ОТВЕТЫ И РЕШЕНИЯ
Блоки
Если грузы уравновешены, то к концам веревки, перекинутой через блок, приложены силы, равные силе тяжести грузов. Очевидно, веревка будет находиться в натянутом состоянии с обоих концов блока. На рисунке же правая веревка нарисована в ненатянутом состоянии так, как будто к ней не приложены никакие силы.
Неподвижный блок применяют для того, чтобы изменить направление действия силы. Например, его удобно использовать для подъема грузов. Прикладывая к веревке, перекинутой через неподвижный блок, силу, направленную вниз, мы заставляем груз подниматься вверх. Нерастяжимая веревка передает это воздействие без изменения вдоль всей своей длины на другой конец грузу. Груз под действием приложенной со стороны веревки силы начинает подниматься. Неподвижные блоки используют в подъемных кранах, полиспастах и огромном количестве других механизмов.
Показания динамометров в положениях А ч В совпадут, так как веревка передает воздействие со стороны груза без изменения вдоль всей своей длины с помощью неподвижного блока независимо от направления. Динамометр покажет силу 20 Н.
В этой задаче цепь нельзя считать невесомой или пренебречь ее весом по сравнению с весом груза. Силы, действующие на неподвижный невесомый блок слева и справа, равны (если нет трения в оси), так как движение груза происходит равномерно, без ускорения. Сила, действующая на левое плечо блока, складывается из веса висящего участка цепи и силы, приложенной со стороны динамометра. Сила с правой стороны блока равна весу груза и весу висящего участка цепи. Так как вес свисающей части цепи на левом рисунке больше, чем на правом, то во втором случае динамометр покажет меньшее значение силы.
Ответ: во втором.
На рисунках показаны только неподвижные блоки. Они не дают выигрыш в силе. Если поднимать груз равномерно, то приложенная к концу веревки сила должна равняться весу груза вместе с суммой сил трения в блоках. На первом рисунке блоков больше. Больше и их сила сопротивления. Поэтому в первой системе надо приложить большую силу.
Ответ: в системе 1.
Понятно, что на рисунке В на оба конца веревок действуют силы величиной 20 Н. Какие же силы действуют на концы веревок в случае /4? На конец левой веревки действует сила 20 Н. Так как система покоится, то на прикрепленный конец правой веревки тоже должна действовать сила 20 Н, иначе бы система двигалась под действием разности сил. Но только эта сила будет действовать не со стороны груза, как в случае В, а со стороны опоры. Это можно понять следующим образом. Левая веревка передает воздействие в 20 Н на свой верхний конец. Далее воздействие через растянутую пружину динамометра передается верхнему концу правой веревки. (Динамометр покоится, следовательно, силы, приложенные к правому и левому его концу, равны.) Правая веревка передает воздействие 20 Н опоре. По третьему закону Ньютона сила, с которой веревка действует на опору, равна по величине силе, с которой опора действует на веревку. То есть с силой 20 Н. Таким образом, обе системы А и В одинаковы с точки зрения действия сил. А раз динамометр А показывает силу 20 Н, то и динамометр В тоже покажет силу 20 Н.
Ответ: 20 Н.
Представим, что человек поднимает себя при помощи блока. На ось блока действует сила, равная весу человека (весом веревок пренебрегаем). Блок неподвижен. Следовательно, равнодействующая всех сил, приложенных к нему, равна нулю. На блок воздействуют две силы натяжения веревки с обоих его концов. Значит, натяжение веревки равно половине силы, приложенной к оси блока, т. е. половине веса человека. Человек, равномерно поднимаясь, прикладывает к веревке такую же силу, с какой веревка воздействует на его руку (3-й закон Ньютона). То есть силу, равную половине его веса. Если человек поднимается по канату или шесту, то при каждом движении он должен прикладывать силу, равную своему весу. Таким образом с помощью блока подниматься легче примерно в 2 раза.
Ответ: при помощи блока легче примерно в 2 раза.
Неподвижный блок не дает выигрыш в силе. Следовательно, нить воздействует на рычаг с силой, равной весу груза. Плечо этой силы равно 4 делениям. Грузы удвоенного веса имеют рычаг, равный 2-м делениям. Условие равновесия выполняется: Р • 4 дел. = 2Р • 2 дел. Система находится в равновесии.
Ответ: да.
В первой системе используются подвижный и неподвижный блоки. Такая комбинация дает выигрыш в силе в два раза. П
оэтому в первой системе к точке А нужно приложить силу, равную половине веса груза. Во второй системе применены два неподвижных блока. Они не дают выигрыш в силе, а только меняют направление ее действия. Поэтому к точке А во второй системе необходимо приложить силу, равную весу груза. Таким образом, в первой системе приложенная сила должна быть в 2 раза меньшей, чем во второй.
Ответ: нет.
Сначала узнаем, какая сила F приложена к рычагу со стороны блока. Ее-плечо равно 3 делениям. Плечо суммарного веса грузов равно 1 делению. Рычаг находится
в равновесии и мы можем применить правило моментов: 6 • 10 Н • 1 дел. = F • 3 дел. Получаем, что F= 20 Н. В системе использован подвижный блок. Он дает выигг рыш в силе в 2 раза. То есть к веревке нужно приложить силу в 2 раза меньшую, чем сила, действующая на ось блока. Поэтому динамометр покажет силу 20 Н : 2 = = 10 Н.
Ответ: 10 Н.
Когда на жертвеннике загорался огонь, он нагревался. Находящийся в нем воздух тоже нагревался и расширялся. Жертвенник, соединенный трубой с кожаным мешком, представлял собой герметичную систему (замкнутый объем). По мере расширения воздуха его давление возрастало. Кожаный мешок постепенно надувался и поднимал камень, лежащий на нем. Этот камень через систему неподвижных блоков и веревку, обвивающую оси дверей, был соединен с другим, более легким камнем. Тот в свою очередь опускался, веревка в натянутом состоянии двигалась, вызывая вращение осей дверей. Двери открывались. Замечательный пример того, как наука служила религии.
Мальчик использует систему блоков, которая дает выигрыш в силе в 2 раза. Он воздействует на конец веревки с силой своего веса Р= mg= 42 кг • 10 м/с2 = 420 Н. Значит вес груза равен 420 Н • 2 = 840 Н.
Ответ: 840 Н.

писать: Т+ FB = FT

Общий вес блока и груза составит 1,2 Н + в Н = 7,2 Н. Именно этот вес будет подниматься с помощью веревки и подвиного блока. Так как подвижный блок дает выигрыш в силе в 2 раза, то сила натяжения веревки (и показания динамометра) будет равна 7,2 Н : 2 = 3,6 Н.
Ответ: 3,6 Н.
Так как подвижный блок дает выигрыш в силе в 2 раза, то прилагая к свободному концу веревки усилие 210 Н, можно поднять груз общим весом 210 Н • 2 = 420 Н. Из них 20 Н составляет вес блока. Значит вес груза Р= 400 Н. Отсюда масса груза
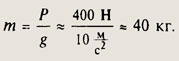
Ответ: 40 кг.
Представим, что груз своим весом Р создает натяжение нити силой Т. По третьему закону Ньютона Т- Р. Подвижные блоки находятся в покое. Значит сумма всех сил, приложенных к ним, равна нулю. Нить (считаем ее нерастяжимой) передает воздействие равномерно по всей своей длине. Так что на блоки с обеих сторон будут действовать силы Т. На ось каждого блока действует вес груза 10 Н. Получаем, что в равновесии 2Т= 10 Н и Т= 5 Н. Отсюда вес противовеса равен Р= Т=5 Н.
Ответ: 5 Н.
Нижний блок является подвижным. Он дает выигрыш в силе в 2 раза. Поэтому в точке А надо приложить силу в 2 раза меньшую, чем та, с которой натянут трос, перекинутый через неподвижный блок. То есть силу в 2000 Н.
Ответ: 2000 Н.

В силу условия нерастяжимости нити, ускорения тел
![]()
равны друг другу по модулю, так как за одно и то же время с момента начала движения тела будут проходить один и тот же путь. а1 = а2 = а. И, наконец, последним следствием того, что нить является невесомой, будет постоянство ускорения а тел, поскольку натяжение нити Т остается неизменным во время движения. Блок закреплен на своей оси и не перемещается относительно точки закрепления. Поэтому на ось со стороны блока действует равнодействующая всех приложенных к нему сил, т. е. сила
![]()
С такой же по модулю силой ось действует на блок. На рисунке эта сила нарисована приложенной к центру блока. В силу перечисленных условий . ясно, что блок растягивает свой подвес с силой 2Т. Теперь перейдем собственно к решению задачи. Свяжем систему координат с поверхностью земли и направим ось О К вертикально вверх. На оба тела действуют две силы — сила тяжести и сила натяжения нити. По второму закону Ньютона произведение массы тела на его ускорение равно векторной сумме всех приложенных к телу сил. Запишем второй закон Ньютона для каждого из тел в векторном виде:
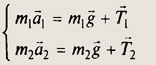
Так как масса m2 второго тела больше массы m1 первого, то второе тело будет опускаться, а первое — подниматься. Направление ускорений показано на рисунке.
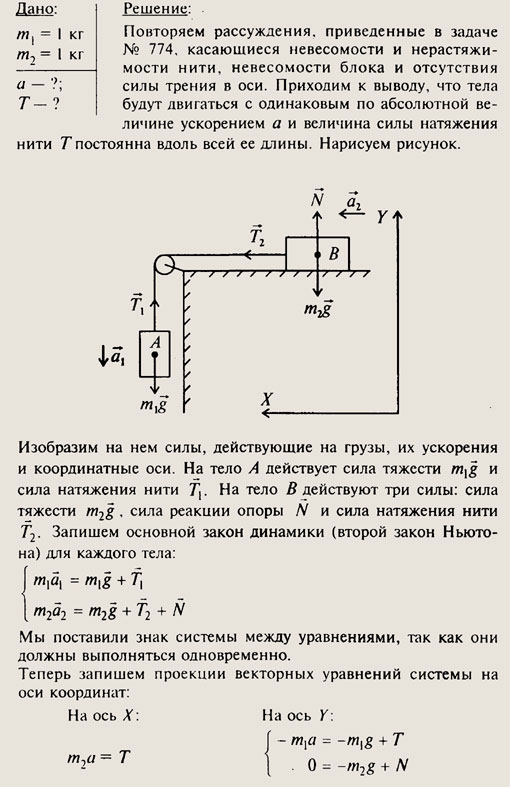
Запишем систему векторных уравнений в проекции на вертикальную ось с учетом равенств, существующих для модулей векторов. Модуль силы берем со знаком минус, если направление силы и оси OY противоположны. Записываем модуль со знаком плюс, когда направление силы и оси О К совпадают. Получаем систему уравнений:




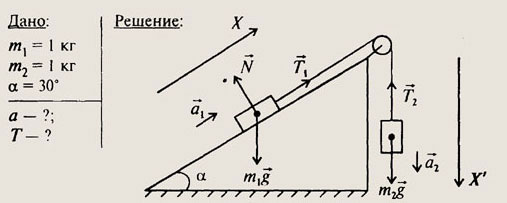
Нарисуем рисунок и изобразим на нем действующие силы. Как и в трех предыдущих задачах (см. № 774), полагаем, что тела движутся с одинаковым по абсолютной величине ускорением а и натяжение нити постоянно вдоль всей ее длины
(а1 = а2 = а и T1 - Т2= Т).
Предположим, что правый груз опускается, а левый поднимается по наклонной плоскости. Правый груз движется под действием двух сил: силы тяжести m2g и силы натяжения нити T2. Левый груз движется по наклонной плоскости под действием трех сил: силы тяжести m1g, силы реакции опоры /V и силы натяжения нити T1. В векторном виде уравнения движения запишутся как система:
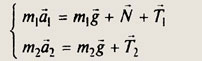
Спроектируем первое уравнение на направление X вдоль наклонной плоскости:
![]()
Спроектируем второе уравнение системы на вертикальное направление X': m2а = m2g — Т. Заметим, что мы всегда можем спроектировать любое векторное уравнение на два независимых направления. Складывая эти два уравнения (они образуют систему), получим выражение
![]()
Из него находим

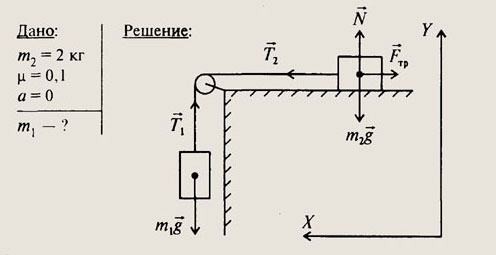
Нарисуем рисунок и изобразим на нем действующие силы. Считаем нить нерастяжимой и невесомой, а блок — невесомым. Трением в оси блока пренебрегаем. Поэтому абсолютное значение силы натяжения нити Т остается постоянным вдоль всей ее длины (T1 = Т2= Т). Свяжем систему координат с поверхностью стола и направим оси, как показано на рисунке. Система грузов движется равномерно, следовательно, ускорение тел равно нулю. Тогда по второму закону Ньютона равнодействующая всех сил, приложенных к телам, равна нулю. На первый груз действует сила тяжести
![]()
и сила натяжения нити T1. На второй груз действует силя тяжести
![]()
сила натяжения нити Т2, сила реакции опоры /V и сила трения Fтр. Таким образом, мы можем написать систему уравнений:
В проекции на вертикальное направление:

Обратимся к рассуждениям, проведенным при решении задачи № 774. Там мы получили, что описанная система воздействует на подвес (в данном случае — пружинные весы) с силой 2T, где Т — сила натяжения нити. В той же задаче мы вывели выражение для Т:
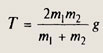
Подставим в него m1 = 1 кг и m2 = 2 кг и получим
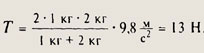
Следовательно, пружинные весы покажут вес Р= 2Т= 26 Н.
Ответ: 26 Н.



В системе использовано два подвижных блока, соединенных последовательно, каждый из которых дает выигрыш в силе в 2 раза. Следовательно, к тросу А надо приложить силу в 4 раза меньшую, чем к тросу В. То есть 1 кН : 4 = 250 Н.
Ответ: 250 Н.
В данной системе два подвижных блока соединены последовательно, т. е. один блок натягивает трос другого. Каждый подвижный блок дает выигрыш в силе в 2 раза, так что общий выигрыш в силе будет четырехкратным. Трос А будет натянут с силой 100 Н • 4 = 400 Н.
Ответ: 400 Н.
