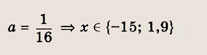Модуль величины. Графики выражений, содержащих модули
• Модулем числа а называется величина, обозначаемая |а| и такая, что

Полезно также напомнить следующее. Пусть заданы функция у - f(x) и ее график. Тогда выражения у = |f(x)|, у = f(|x|) и |у| = f(x) определяются следующим образом:
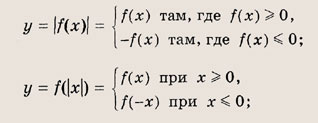
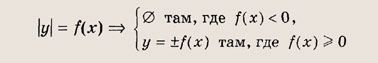
Графики функции у = f(x) и этих выражений приведены ниже.
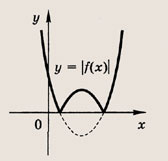
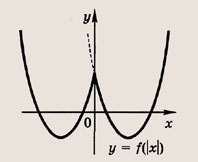
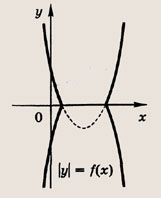
Графики соотношений, содержащих большее число знаков модуля, строим, последовательно выполняя приведенные выше построения.
В заданиях 1—6 постройте графики следующих функций и уравнений:
а) у = f(x);
б) у = |f(x)|;
в) у = f(|x|);
г) |у| = f(x);
д) у = |f(|х|)|;
е) |у| = f(|х|);
ж) |у| = |f(x)|
з) |у| = |f(|x|)|
Задание 1.
у = 2х-3
Ответ:
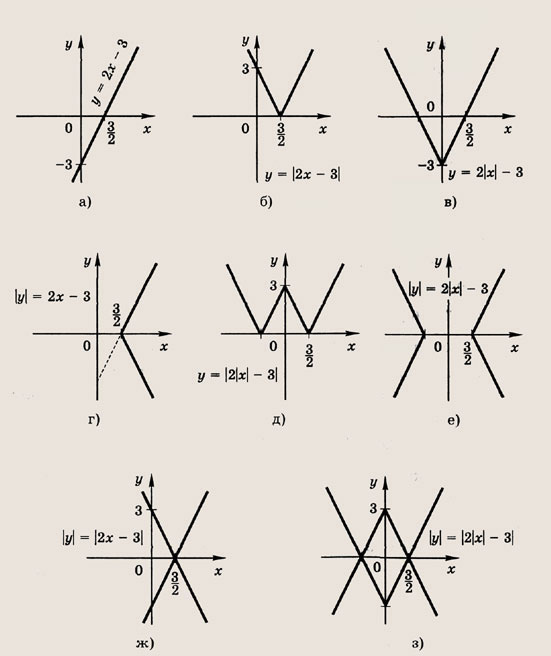
Задание 2.
у = 3-х
Задание З.
у = х2- 4х + 3
Ответ:
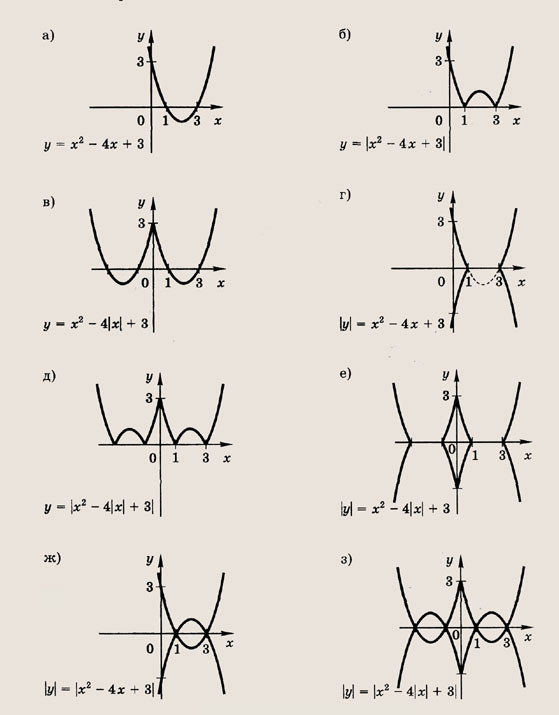
Задание 4.
у = 3х- х2
Задание 5.
![]()
Ответ:
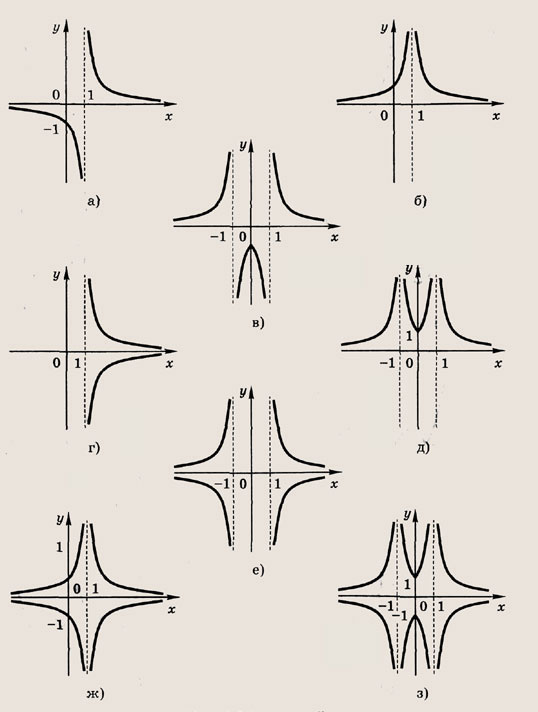
Задание 6.
![]()
Ответ:
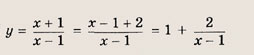
Постройте графики следующих функций и уравнений (7-26):
Задание 7.
у = |х|(х - 2)
Ответ:
Задание 8.
у = х|х - 3|
Ответ:
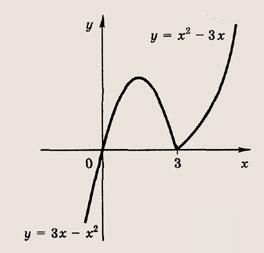
Задание 9.
у = 2|х + 2| - х - 3| - х
Ответ:
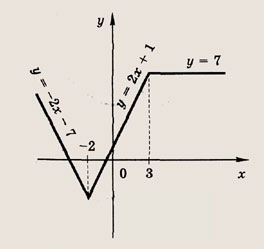
Задание 10.
у = -|х + 2| + 2|х - 1| + х
Ответ:
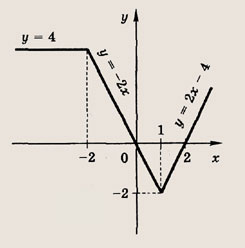
Задание 11.
![]()
Ответ:
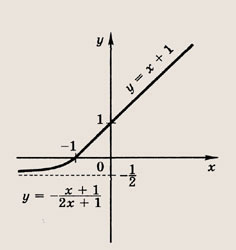
Задание 12.
![]()
Ответ:
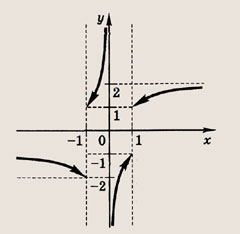
Задание 13.
![]()
Ответ:
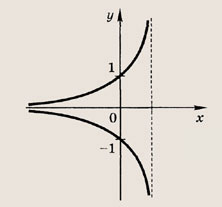
Задание 14.
![]()
Ответ:
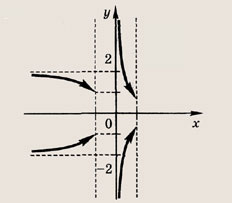
Задание 15.
![]()
Ответ:
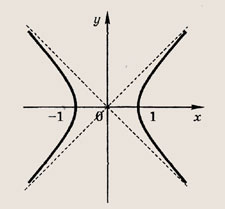
Задание 16.
![]()
Ответ:
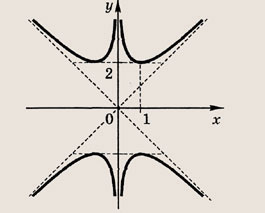
Задание 17.
|x| + 2|y| = 4
Ответ:
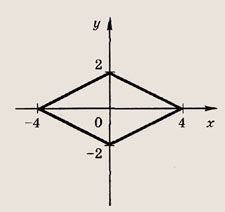
Задание 18.
|x - 2| + 2| у + 1| = 4
Ответ:
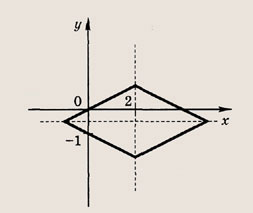
Задание 19.
|x + 2| - |y + 1| = 2
Ответ:
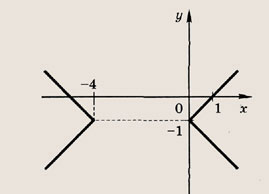
Задание 20.
2|x - 2| - |y + 1| = 3
Ответ:
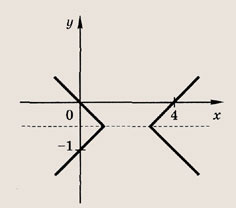
Задание 21.
|x + у| + |x - y| = 6
Ответ:
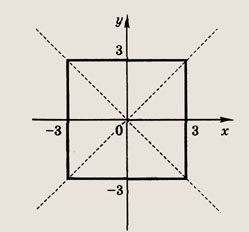
Задание 22.
|x + 2y| + |2x -y| = 6
Ответ:
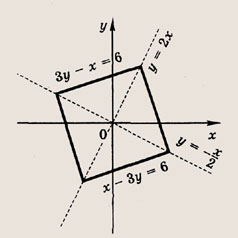
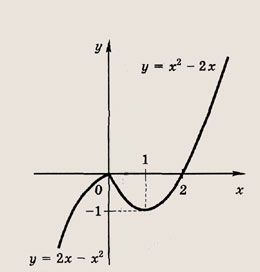
Задание 23.
|2x + y| + |x - у - 3| = 1
Ответ:
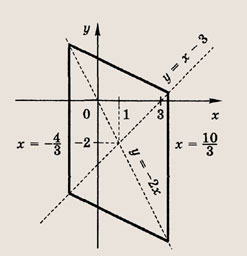
Задание 24.
|x - 2y + 1| + |y + 2x - 3| = 5
Ответ:
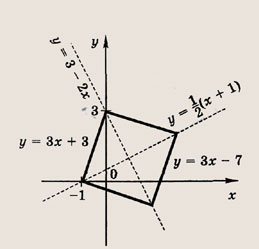
Задание 25.
(|х| - 1)2+ (у - 2)2 = 4
Ответ:
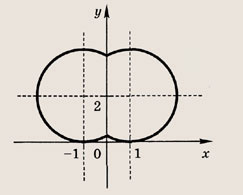
Задание 26.
(Iх| -2)2+ (|у| -1)2= 4
Ответ:
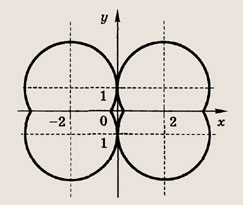
На координатной плоскости отметьте штриховкой множество точек, координаты которых удовлетворяют следующим неравенствам (27—40):
Задание 27.
![]()
Ответ:
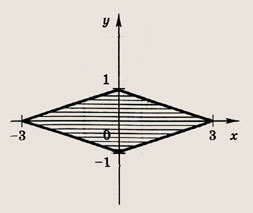
Задание 28.
![]()
Указание:
Выполните параллельный перенос фигуры, построенной в задании 27.
Задание 29.
![]()
Ответ:
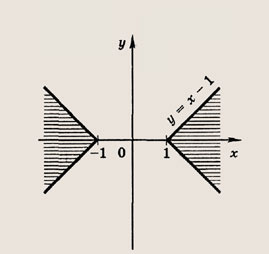
Задание 30.
![]()
Указание:
Выполните параллельный перенос фигуры, построенной в задании 29.
Задание 31.
![]()
Ответ:
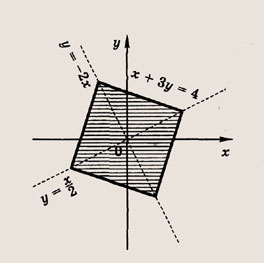
Задание 32.
![]()
Ответ:
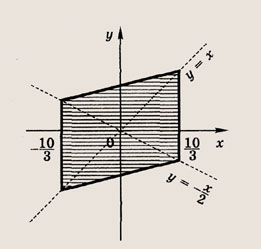
Задание 33.
![]()
Ответ:
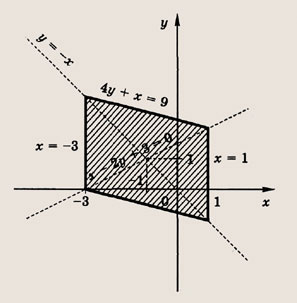
Задание 34.
![]()
Ответ:
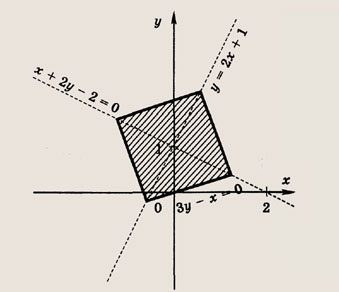
Задание 35.
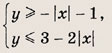
Ответ:
Задание 36.

Ответ:
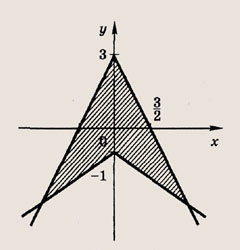
Задание 37.
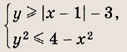
Ответ:
Задание 38.
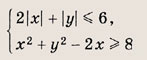
Ответ:
Задание 39.
![]()
Ответ:
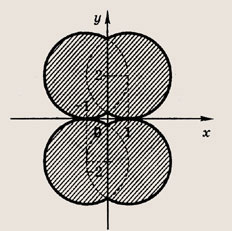
Задание 40.
![]()
Указание:
Выполните параллельный перенос фигуры, построенной в задании 39.
Найдите площадь фигуры, которая задается на координатной плоскости следующими соотношениями (41—46).
Задание 41.
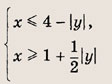
Ответ:
SABCD = 6
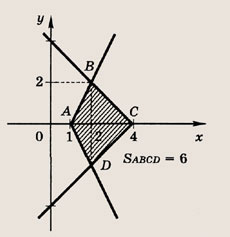
Задание 42.
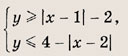
Решение:
Фигура, определяемая заданными неравенствами, — прямоугольник ABCD
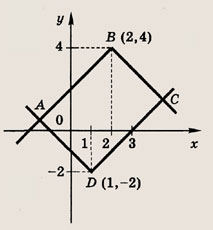
Стороны прямоугольника лежат
на следующих прямых: (АB) на у = х + 2; (ВС) на у = 6 - х; (DC)
на у = х - 3; AD на у = -1 - х. Координаты вершин:
![]()
В (2; 4),
![]()
D (1; -2)
Тогда
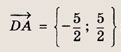
![]()
откуда:
![]()
![]()
![]()
Ответ:
![]()
Задание 43.
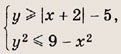
Указание:
![]()
Ответ:
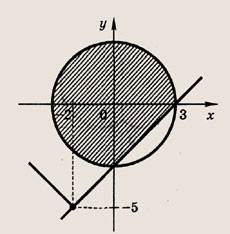
Задание 44.
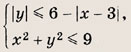
Ответ:
![]()
Задание 45.
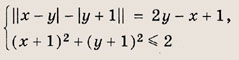
Решение:
Запишем данное равенство в виде
||у - х - |у + 1|| = (у - х) + (у + 1)
Это равенство справедливо только в том случае, если пара чисел (х; у) удовлетворяет одной из следующих систем неравенств:
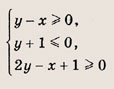
Отметим штриховкой в плоскости (х ; у) множество точек, координаты которых удовлетворяют этим неравенствам, а также неравенству
(х + 1)2 + (у + 1)2< 2
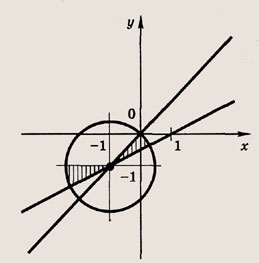
Мы видим, что площадь заштрихованной области равна
![]()
площади круга радиуса
![]()
Следовательно, искомая площадь равна
![]()
Ответ:
![]()
Задание 46.
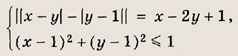
Указание:
См. решение задания 45.
Ответ:
![]()
Задание 47.
При каких значениях р площадь фигуры, заданной на координатной плоскости условием
![]()
равна 24?
Решение:
Очевидно, что р > 0. Перепишем неравенство в виде
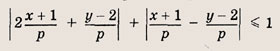
и выполним замену переменных, полагая
![]()
![]()
Построим фигуру, задаваемую в плоскости переменных (u; v) неравенством
![]()
и найдем ее площадь
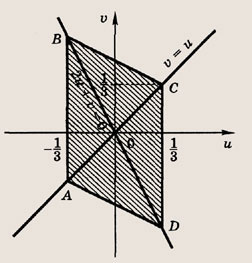
Легко установить, что это параллелограмм. Сторона DC параллельна координатной
оси Оv и равна по длине 1. Высота параллелограмма равна
![]()
а его площадь
![]()
Фигура
![]()
получается из построенной растяжением вдоль обеих осей в р раз. Следовательно,
ее площадь
![]()
Таким образом, и площадь фигуры, задаваемой неравенством
![]()
равна
![]()
поскольку она получается параллельным переносом из фигуры
![]()
Теперь вычисляем требуемое значение
![]()
Ответ:
р = 6
Задание 48.
Найдите площадь фигуры, которая задается на координатной плоскости системой неравенств
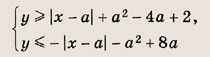
При каких значениях а эта площадь является наибольшей?
Решение:
Положим u = х - a; v = у - (а2 - 4а + 2), Тогда площадь исходной фигуры будет равна площади фигуры, задаваемой неравенствами
![]()
Эти неравенства задают непустое множество лишь при выполнении условия
![]()
т. е. при
![]()
При этих значениях а получаем квадрат с диагональю |ОА| = 12a - 2а2 - 2
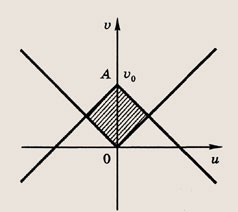
Его площадь S = 2(а2 - 6а + 1)2. Наибольшее значение площадь квадрата принимает при а = 3. Имеем Smax = S(3) = 128.
Ответ:
S(a) = = 2(a2 - 6a + 1)2, Smax = 128 при а = 3.
Задание 49.
При каких значениях а система
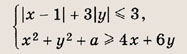
имеет хотя бы одно решение?
Ответ:
![]()
Задание 50.
При каких значениях а система
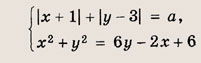
имеет хотя бы одно решение?
Указание:
Постройте графики данных уравнений и проследите, как меняется график первого уравнения при изменении параметра а.
Ответ:
![]()
Решите следующие уравнения
и системы уравнений (51—66):
Задание 51.
|х-3| + 2|х+1| = 4
Ответ:
{-1}
Задание 52.
|х + 5| + |х - 8| = 13
Ответ:
[-5;8]
Задание 53.
2|х-5| = 3|2х - 5| - 4|х - 1| + 1
Ответ:
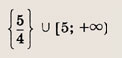
Задание 54.
|х| + |х - 2| + |2х - 1| = 4х - 1
Решение:
Раскрывая знак модуля, получаем на каждом из указанных ниже интервалов:
1) при
![]()
откуда
![]()
2) при
![]()
откуда
![]()
3) при
![]()
откуда х = 1;
4) при
![]()
откуда получаем, что
![]()
Ответ:
1
Задание 55.
3||х - 1| = 3|х| - 2
Указание:
См. решение задания 56.
Ответ:
![]()
Задание 56.
||х2 - Зх| - 5| = х - 1
Решение:
Данное уравнение равносильно совокупности двух систем:
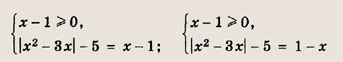
Для первой из них записываем равносильную совокупность двух систем:
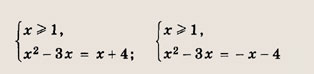
Решив эти системы, получаем
![]()
Аналогично вторая система равносильна следующей совокупности:
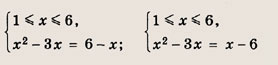
откуда
![]()
Ответ:
![]()
Задание 57.
х|х| + 2| х - 2| = 3
Ответ:
![]()
Задание 58.
|х2 - 4х| = х2 + х - 5| - 3
Ответ:
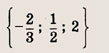
Задание 59.
|х2 - 2х -3| + 2|х -2| = 5
Решение:
Запишем уравнение в виде
|х - 3||х + 1| + 2|х - 2| = 5
Раскрывая знак модуля на каждом из указанных ниже интервалов, получаем:
1)
х < -1 => х2 - 2х - 3 - 2х + 4 = 5, т. е. х2 - 4х - 4 = 0, откуда
![]()
Однако оба эти корня не удовлетворяют условию х < -1.
2)
![]()
т. е. х2 = 2, откуда
![]()
В ответ войдет только значение
![]()
3)
![]()
т. е. х2 - 4х + 6 = 0. Это уравнение решений не имеет.
4)
х > 3 => х2 - 2х - 3 + 2х - 4 = 5, т. е. х2 = 12. Учитывая условие х > 3, получаем
![]()
Ответ:
![]()
Задание 60.
|х2 - х|+ |х2 - Зх + 2| = 2
Ответ:
{0; 2}
Задание 61.
![]()
Указание:
х = 0 не входит в область допустимых значений.
Ответ:
{8}
Задание 62.
![]()
Указание:
х = 1 не входит в область допустимых значений.
Ответ:
![]()
Задание 63.
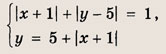
Ответ:
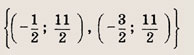
Задание 64.
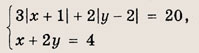
Решение:
Из второго уравнения имеем, что 2у — 4 = -х. Подставив это выражение в первое равенство, получим
3|х + 1| + х = 20, откуда
следует:
1)
![]()
т.е.
![]()
тогда
![]()
2)
![]()
не подходит;
3)
х > 0 ==> Зх + 3 + х = 20, т. е.
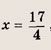
тогда
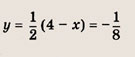
Ответ:
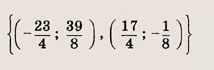
Задание 65.
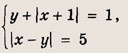
Ответ:
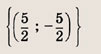
Задание 66.
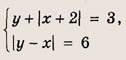
Решение:
Данная система равносильна совокупности
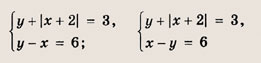
Первая из этих систем приводит к уравнению |х + 2| = - х - 3, которое не имеет решений. Решаем вторую систему. Подставляя у = х - 6 в первое уравнение, получаем |х + 2| = 9 - х, откуда
![]()
а тогда
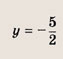
Ответ:
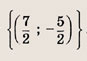
Задание 67.
Функция f(x) определена на всей числовой оси, является нечетной, периодической с периодом 4 и на отрезке [0; 2] ее значения вычисляются по формуле f(x) = 1 - |х - 1|. Решите уравнение
2f(x)f(x - 8) - 5f(x + 12) + 2 = 0
Решение:
Используя перио- у личность f(x), записываем уравнение в виде 2(ƒ(х))2 - 5ƒ(x) + 2 = 0, откуда
![]()
Далее, используя условие, получим
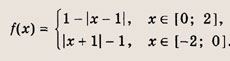
График функции у = ƒ(x) на [-2, -2] изображен на рис.
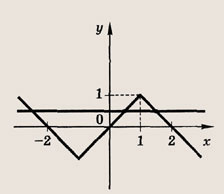
Теперь решаем уравнения:
1 - [х - 1| = 2, откуда х € 0;
![]()
откуда
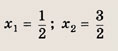
Эти решения будут повторяться с периодом, равным 4.
Ответ:
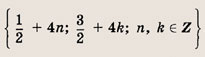
Задание 68.
Функция f(x) определена на всей числовой оси, является четной, периодической с периодом 4 и на отрезке [0; 2] ее значения вычисляются по формуле f(x) = |х - 1| - 1. Решите уравнение
2f(x + 4)f(x) + 5f(x + 16) + 2 = 0
Указание:
См. решение задания 67.
Ответ:
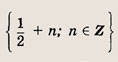
Задание 69.
Найдите все значения а, при каждом из которых все решения уравнения 4 |х - За| + 6а - 24 + х = 0 принадлежат отрезку [6; 12]. Найдите эти решения.
Решение:
Данное уравнение равносильно совокупности двух следующих систем:
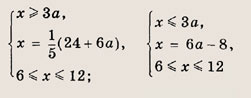
Решение первой системы дает:
![]()
при
![]()
второй х = 6а - 8 при
![]()
Объединяя решения, получаем ответ.
Ответ:
при
![]()
при
![]()
при
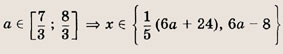
Задание 70.
Найдите все значения а, при каждом из которых все решения уравнения 3|х + 2а| - За + х - 15 = 0 принадлежат отрезку [4; 9]. Найдите эти решения.
Ответ:
При
![]()
при
![]()
при
![]()
Задание 71.
При всех значениях а решите уравнение
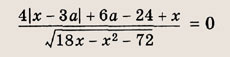
Ответ:
при
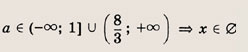
при
![]()
при
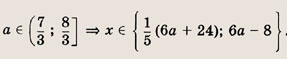
Указание:
Должно выполняться неравенство 18х - х2 - 72 > О, откуда
![]()
Далее см. решение задачи 69.
Задание 72.
При всех значениях а решите уравнение
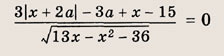
Ответ:
при
![]()
при
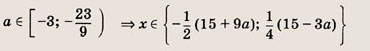
при
![]()
При решении задач 73—76 используйте следующие простые неравенства, справедливые
для любых чисел и и v:
![]()
Подумайте, когда выполняются равенства?
Задание 73.
Найдите все а, при которых среди решений уравнения
2 |х - а| + |2х - а - 6| = |6 - а|
имеется ровно одно целое число.
Решение:
Положим u = 2х - 2а, v = 2х - а - 6. Тогда уравнение примет вид |u| + |v| = |u — v|, а также равенство выполняется только в том случае, если и и v имеют разные знаки. Следовательно, исходное уравнение равносильно совокупности систем неравенств:
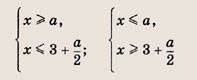
Отметим в плоскости (а, х) штриховкой область, в которой выполняются эти неравенства.
Мы видим, что при а = б уравнение имеет в качестве целочисленного решения только число х = 6. Далее находим, что

и т. д., а также
![]()
и т. д. Единственное целое решение уравнение будет иметь лишь при
![]()
Ответ:
![]()
Задание 74.
Найдите все а, при которых среди решений неравенства
![]()
имеются ровно два натуральных числа.
Указание:
Неравенство выполнено только в том случае, если выражения (х - а - 3) и (х + 2а - 9) имеют разные знаки (в этом случае выполняется равенство). Далее см. решение задания 73.
Ответ:
![]()
Задание 75.
При каких а система уравнений
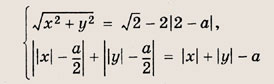
имеет хотя бы одно решение?
Решение:
Для выполнения первого равенства необходимо, чтобы
![]()
откуда
![]()
При этих значениях а график первого уравнения — окружность с центром О(0; 0) и радиусом
![]()
Обозначив
![]()
запишем второе уравнение в виде |u| + |v| = u + v. Последнее равенство справедливо
только при
![]()
т. е. при
![]()
Отметим в плоскости (х; у) штриховкой эту область.
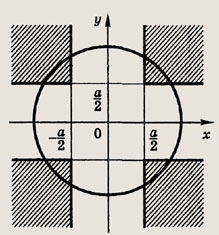
Окружность
![]()
пересекает с заштрихованной областью (т.е. исходная система имеет решения) при
выполнении неравенства
![]()
Это неравенство выполняется лишь при а = 2, поскольку
![]()
это число и является решением.
Ответ:
{2}.
Задание 76.
При каких а система неравенств
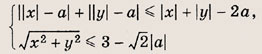
имеет хотя бы одно решение?
Указание:
Первое неравенство справедливо только в том случае, если
![]()
Далее рассмотрите отдельно случай
![]()
При а > 0 решение аналогично решению задания 75.
Ответ:
![]()
• Использование графических методов (построение графиков, штриховка областей, отвечающих условиям задач) существенно облегчает решение приведенных ниже задач.
Установите, сколько решений в зависимости от а имеют следующие уравнения (77—84):
Задание 77.
||х - 1| - 2| = а
Ответ:
При
![]()
=> нет решений; при
![]()
два решения; при
![]()
четыре решения; при а = 2 => три решения.
Задание 78.
2 |х| + | х - 1| = а
Ответ:
При
![]()
нет решений, при а = 1 => одно решение; при
![]()
два решения.
Задание 79.
х|х - 4| = а
Решение:
Имеем
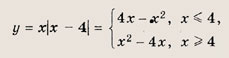
График этой функции изображен на рис.
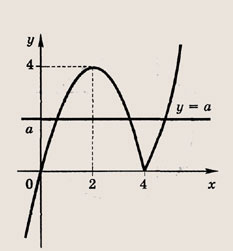
Ответ:
при
![]()
одно решение; при
![]()
два решения; при
![]()
три решения.
Задание
80.
|х2 - 4х + 3| = а(х - 1)
Решение:
Запишем уравнение в виде |х - З||х - 1| = а(х - 1). Отметим, что х = 1 — решение этого уравнения при любом а. Теперь построим график функции.
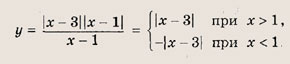
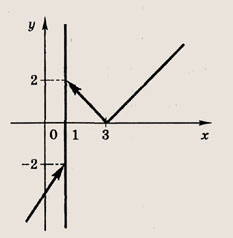
Ответ:
при
![]()
два решения; при
![]()
одно решение; при
![]()
три решения.
Задание 81.
|х3 + 8| = а(х + 2)
Ответ:
При
![]()
два решения; при
![]()
одно решение; при
![]()
три решения.
Задание 82.
|х4 - 16| = а(4 - х2)
Решение:
Запишем уравнение в виде
(х2 + 4)|4 - х2| = а(4 - х2)
Отметим, что числа х = ±2 - решения этого уравнения при любом а. Далее рассмотрим функцию
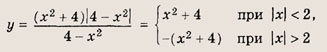
Построим ее график
и запишем ответ.
Ответ:
при
![]()
четыре решения; при
![]()
два решения; при а = 4 => три решения; при
![]()
четыре решения; при
![]()
два решения.
Задание 83.
![]()
Ответ:
При
![]()
нет решений; при а = 2 => два решения; при
![]()
четыре решения.
Задание 84.
![]()
Ответ:
При
![]()
нет решений; при а = 0 => одно решение; при
![]()
два решения; при
![]()
три решения; при
![]()
четыре решения.
Задание 85.
При каких значениях а уравнение 3|х - 1| + 2 = ах имеет ровно два решения?
Ответ:
(2;3)
Задание 86.
При каких значениях а уравнение 2|х + 3| - 3|х + 4| + 3| х + 5| = ах имеет два различных решения?
Решение:
Построим график функции у = 2|х + 3| - 3|х + 4| + 3|х + 5|.
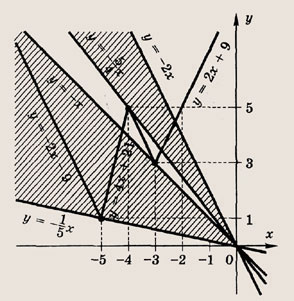
Штриховкой отметим те углы, в которых прямая у = ах пересекает построенный график ровно в двух точках.
Ответ:
![]()
Задание 87.
При каких значениях а уравнение х|х + 2а| = а - 1 имеет единственное решение?
Решение:
Рассмотрим два случая.
1) Пусть а < 0. Построим график функции у = х|х + 2а|.
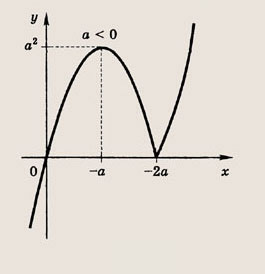
Тогда уравнение имеет единственное решение, если а - 1 < 0 или если а - 1 > а2. Второе неравенство решений не имеет. Получаем, что подходят все значения а < 0. Очевидно, также подходит а = 0.
2) Пусть а > 0.
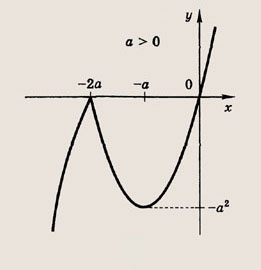
Тогда уравнение имеет единственное решение при а - 1 > 0, т. е. а > 1, а также в случае, если а - 1 < -а2, т. е. а2 + а - 1 < 0. Решая последнее неравенство и учитывая, что а > 0, получаем
![]()
Объединяя все решения, записываем ответ:
Ответ:
![]()
Задание 88.
При каких значениях а уравнение
|х2 - 2х| + |х2 - Зх + 2| = х2 - 4х + а
имеет ровно три различных решения?
Решение:
Запишем уравнение в виде
|х2 - 2х| + |х2 - Зх + 2| - |х - 2|2 = а - 4, т. е.
|х - 2|(|х| + |х - 1| - |х - 2|) = а - 4
и построим график левой части этого уравнения.
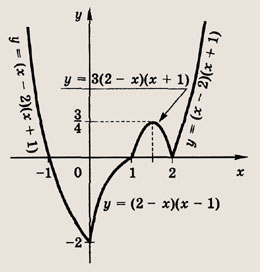
Получаем кривую, состоящую из кусков парабол. Три решения получаются только в том случае, если а - 4 = 0 или
![]()
Значит, что
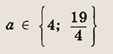
Ответ:
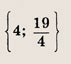
Задание 89.
При каких а система уравнений
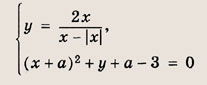
имеет единственное решение?
Решение:
![]()
при х< 0, а при
![]()
эта функция не определена.
Графиком функции у = -(х + а)2 + 3 - а — является парабола с вершиной
А (-а; 3 - а).
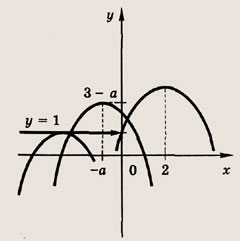
Точка пересечения графиков будет единственной, если
![]()
либо у(-а) = 1. Неравенство
![]()
т. е.
![]()
дает а € [-2; 1]. Число а = -2 следует исключить, поскольку в этом случае парабола пересекает ось Оу левой ветвью в точке у = 1, т. е. система не имеет решений. Уравнение у(-а) = 1 имеет вид 3 - а = 1, откуда а = 2.
Ответ:
![]()
Задание 90.
При каких а система уравнении
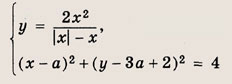
имеет хотя бы одно решение?
Решение:
Имеем
![]()
при х < 0; (х - а)2 + (у - За + 2)2 = 4 — окружность радиуса 2, центр которой М(а; За - 2) с изменением а движется по прямой у = Зх - 2.
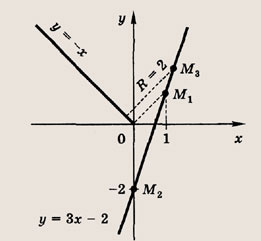
Точкой пересечения прямой у = х (перпендикуляра к у = -х в точке О(0; 0)) и прямой у = Зх - 2 является точка М1(1; 1). Расстояние от М1 до О равно
![]()
Поэтому окружность будет пересекаться с лучом у = -х(х < 0) только в том
случае, если ее центр М(а; За - 2) расположен на прямой у = Зх - 2 между точкой
М2(0; -2), расстояние от которой до О(0, 0) равно 2, и точкой М3,
где М3 — центр окружности радиуса 2, касающейся луча у = -х(х <
0), включая саму точку М3.
Так как у = -х — касательная к окружности (х - а)2 + (у - За + 2)2 = 4, то уравнение
(х- а)2 + (-х- За + 2)2=4
должно иметь единственное решение. Раскрывая скобки и приводя подобные члены, приравнивая дискриминант квадратного трехчлена нулю, получаем
![]()
Следует взять положительное значение а, т. е.
![]()
Легко видеть, что точка М2 получается при а = 0.
Ответ:
![]()
Задание 91.
При каких а уравнение
|х2 - 6х + 5| = ах - 1
имеет единственное решение?
Ответ:
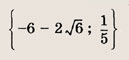
Решите следующие уравнения (92—98):
Задание 92.
|х - 1| + 2х = а
Ответ:
При
![]()
при
![]()
Задание 93.
х|х - 4| = а
Решение:
Построим график функции у = х|х - 4| и найдем абсциссы точек пересечения этого графика с прямой у = а
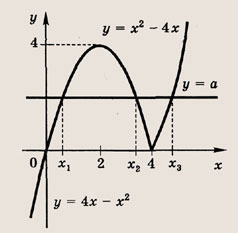
Имеем: х1 и х2 — корни уравнения 4х - х2 = а, т. е. х2 - 4х + а = 0, откуда
![]()
х3 - больший корень уравнения х2 - 4х - а = 0, откуда
![]()
Ответ:
при
![]()
при
![]()
при
![]()
![]()
при
![]()
![]()
при
![]()
Задание 94.
|х+1 + а|х - 2| = 3
Ответ:
при
![]()
при
![]()
при
![]()
х = 2
при
![]()
Задание 95.
|х2 - 4х + 3| = а|х - 1|
Указание:
Запишите уравнение в виде |х - 3||х - 1| = а|х - 1|.
Ответ:
при
![]()
при
![]()
при
![]()
при
![]()
при
![]()
Задание 96.
х2 + Зх = |а(х + 3)|
Решение:
Запишем уравнение в виде х(х + 3) = |а||х + 3|. Отметим, что х = -3 — решение уравнения при любом а. Если
![]()
то
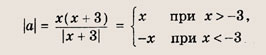
Построим график этого уравнения.
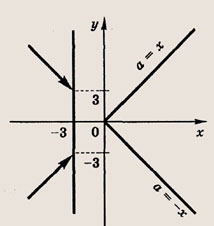
Ответ:
при
![]()
при
![]()
при
![]()
при
![]()
Задание 97.
х2 + |х + а| - 2 = 0
Решение:
Раскрывая модуль, получаем
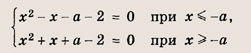
Решим эти уравнения:
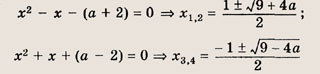
Строим график:
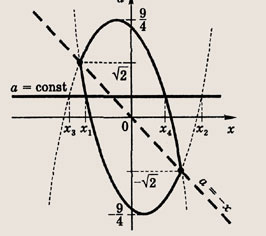
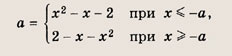
Ответ:
при
![]()
при
![]()
при
![]()
при
![]()
при
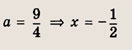
при
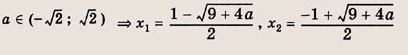
Задание 98.
а(х - 1)2 - х - 3| + 2 = 0
Ответ:
При
![]()
при
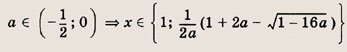
при
![]()
при
![]()
при