Варианты проверочных работ
Вариант 1
Задание 1.
Разделите многочлен
2х4 + х3 - 5х2 - х + 1 на х2 - х.
Укажите частное и остаток.
Ответ:
Решите следующие уравнения и системы уравнений (2-5):
Задание 2.
![]()
Задание 3.
2х3 + х2 - 4х - 2 = 0
Задание 4.
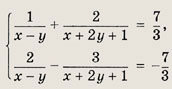
Задание 5.
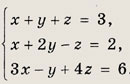
Задание
6.
Если двузначное число разделить на число, записанное теми же цифрами, но в обратном порядке, то в частном получится 4, а в остатке 15. Если же из данного числа вычесть 9, то получится сумма квадратов цифр этого числа. Найдите это число.
Задание 7.
При каких значениях а и b многочлен Зх3 + 2ах2 -- bх + 4 делится на х2 + 1 без остатка?
Задание 8.
Найдите все а, при которых система
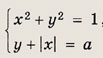
имеет ровно четыре решения.
Вариант 2
Решите следующие уравнения и системы уравнений:
Задание 1.
(х + 1)(х2 + 2) + (х + 2)(х2 + 1) = 2
Задание 2.
(х - З)4 + (х - 5)4 = 82
Задание 3.
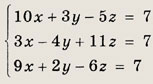
Задание 4.
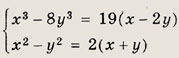
Задание 5.
Если двузначное число разделить на сумму его цифр, то получится в частном бив остатке 2. Если же это число разделить на произведение его цифр, то получится в частном 5, а в остатке 2. Найдите это число.
Задание 6.
При каких а и b многочлен х4 + ах3 + bх2 - 8х + 1 является точным квадратом другого многочлена?
Задание 7.
При каких а система уравнений
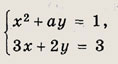
имеет единственное решение?
Задание 8.
Сколько решений в зависимости от а имеет уравнение
|х4 - 1| = а(х2 - 1)?
Вариант 3
Решите следующие уравнения и системы уравнений:
Задание 1.
4x3 - 24x2 + 21x - 5 = 0
Задание 2.
![]()
Задание 3.
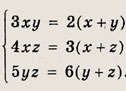
Задание 4.
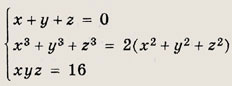
Задание 5.
При каких значениях а система уравнений
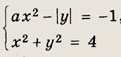
не имеет решений?
Задание 6.
Сколько решений в зависимости от а имеет уравнение
|х4 - 16| = а(4 - х2)?
Задание 7.
При каких значениях а для любого b найдется хотя бы одно с такое, что система уравнений
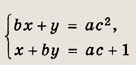
имеет хотя бы одно решение?
Задание 8.
При каких значениях а и b существуют два различных корня уравнения х3 - 5х2 + 7х = а, являющихся одновременно и корнями уравнения х3 - 8х + b = 0?
