Варианты проверочных работ
Вариант 1
Решите неравенства:
Задание 1.
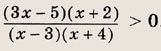
Задание 2.
![]()
Задание 3.
![]()
Задание 4.
|x - 1| - 3 > x - |x - 2|
Задание 5.
Найдите все с € R, для каждого из которых числа х и у, удовлетворяющие системе
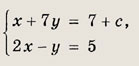
удовлетворяют также неравенству х > у - 2.
Задание 6.
На координатной плоскости (х, у) отметьте штриховкой область, задаваемую неравенствами
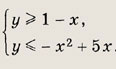
Задание 7.
При каких а из неравенства х2 - (За + 1)x + а > 0 следует неравенство x > 1?
Задание 8.
Решите неравенство
![]()
Вариант 2
Решите неравенства и системы неравенств:
Задание 1.
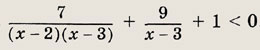
Задание 2.
![]()
Задание 3.
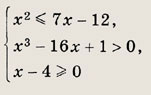
Задание 4.
![]()
Задание 5.
На координатной плоскости отметьте штриховкой область, задаваемую неравенствами
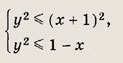
Задание 6.
Найдите все а, при которых неравенство
![]()
выполняется для всех пар (х; у) таких, что |х| = |у|.
Задание 7.
При каких а все решения неравенства ах2 - х + 2 -- 4а < 0 принадлежат интервалу (0; 2)?
Задание 8.
Решите неравенство ||х| - 1| < 2ах.
Вариант 3
Решите неравенства:
Задание 1.
![]()
Задание 2.
![]()
Задание 3.
Зх2(х - 4)2< 32 - 5(х - 2)2
Задание 4.
Числа х и у удовлетворяют системе неравенств:
![]()
Найдите наибольшее значение величины х2 + у2.
Задание 5.
Найдите все значения х, при которых неравенство
(2с - 6)х2 + (32 - 10с)х - (8 + с) < 0
выполняется для всех с € (2; 4).
Задание 6.
Решите неравенство |1 - |x|| < а - x.
Задание 7.
При каком а система неравенств
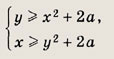
имеет единственное решение?
Задание 8.
Найдите все значения параметра а, при каждом из которых число целочисленных решений неравенства
![]()
максимально.
