Линейное уравнение. Прямая и окружность
С линейным уравнением ах + b = 0 (а, b — заданные числа — коэффициенты уравнения, х — искомая переменная величина) мы встречаемся с первых шагов изучения курса алгебры. Если
![]()
то такое уравнение имеет единственное решение
![]()
Изучение геометрии начи нается с изучения свойств прямых и окружностей. Это
не случайно. Ведь окружающий нас мир во многих своих проявлениях линеен, а окружность
— одна из самых распространенных в нем линий.
Рекомендуем всем решить задачи 1—73 и варианты 1 и 2 проверочных работ (например, четные номера на занятиях с преподавателем, а нечетные — самостоятельно). Если вы решили поступить в вуз с высокими требованиями по математике, то обратите внимание на задачи 74—80 и вариант 3.
Решите уравнения 1—24. Это либо линейные, либо сводящиеся к линейным простыми преобразованиями уравнения.
Задание 1.
-4х = 5
Ответ:
-1,25
Задание 2.
![]()
Ответ:
![]()
Задание 3.
0,3х = -0,81
Ответ:
-2,7
Задание 4.
![]()
Ответ:
4
Задание 5.
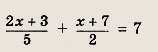
Ответ:
![]()
Задание 6.
![]()
Ответ:
-0,2
Задание 7.
![]()
Ответ:
![]()
Задание 8.
![]()
Ответ:
2
Задание 9.
![]()
Ответ:
![]()
Задание 10.
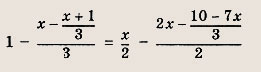
Ответ:
![]()
Задание 11.
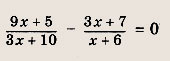
Ответ:
5
Задание 12.
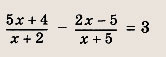
Ответ:
0
Задание 13.
![]()
Ответ:
![]()
Задание 14.
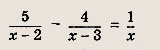
Ответ:
-3
Задание 15.
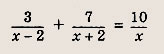
Ответ:
5
Задание 16.
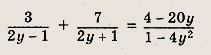
Ответ:
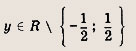
Задание 17.
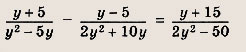
Ответ:
![]()
Задание 18.
![]()
Ответ:
![]()
Задание 19.
![]()
Ответ:
0
Задание 20.
![]()
Ответ:
![]()
Задание 21.
(Зх - 1)2 - 5(2х + 1)2 + (6x - 3)(2x +1) = (х- I)2
Ответ:
![]()
Задание 22.
(x + 6)2(x + 1) - (x - 3)2 (x + 10) = (3х + 4)2
Ответ:
![]()
Задание 23.
(х + 2)3-х(х + 3)2=23
Ответ:
5
Задание 24.
(x + 2)3 - (x - 2)3 = 12(x - 2)(x + 3)
Ответ:
![]()
Следующие системы уравнений (25—30) решите, сведя их подстановками к линейным уравнениям. Текстовые задачи данной темы (31—37) также приводят к линейным уравнениям.
Задание 25.
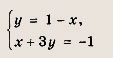
Ответ:
(2;-1)
Задание 26.
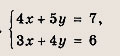
Ответ:
(-2;3)
Задание 27.
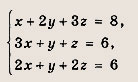
Ответ:
(1;2;1)
Задание 28.
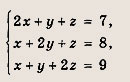
Ответ:
(1;2;3)
Задание 29.
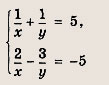
Ответ:
![]()
Задание 30.
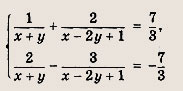
Ответ:
(2;1)
Задание 31.
Сумма цифр двузначного числа равна 15. Если прибавить к нему 27, то получится число, записанное теми же цифрами, но в обратном порядке. Найдите это двузначное число.
Ответ:
69
Задание 32.
Числитель дроби на 2 меньше знаменателя. Если числитель дроби уменьшить на 1, а знаменатель увеличить на 3, то значение дроби будет равно 0,25 Найдите дробь.
Ответ:
![]()
Задание 33.
Моторная лодка прошла против течения реки 16 км и вернулась обратно, затратив на обратный путь на 40 мин меньше, чем на путь против течения. Найдите собственную скорость лодки, если скорость течения реки равна 2 км/ч.
Ответ:
10 км/ч
Задание 34.
Производительность косилки в 5 раз выше, чем производительность бригады косарей. Сколько дней потребуется бригаде косарей, чтобы скосить луг, если известно, что самоходная косилка и бригада косарей, работая вместе, смогут закончить сенокос за 3 дня?
Ответ:
18
Задание 35.
Пенсионер в начале года положил 1200 р. в два банка. В первом банке начисляли 50% годовых, а во втором — 40% Сколько рублей положил пенсионер в каждый банк, если в конце года он получил 1760 р.?
Ответ:
800 р. и 400 р.
Задание 36.
За некоторое время количество акций гражданина Иванова увеличилось на 20% . На сколько процентов увеличилась цена каждой акции гражданина Иванова, если общая стоимость всех его акций возросла на 38% ?
Ответ:
15%
Задание 37.
От кусков массой 6 кг и 12 кг двух сплавов с различным процентным содержанием меди отрезали по куску равной массы. Каждый из отрезанных кусков сплавили с остатком куска другого сплава, после чего процентное содержание меди в обоих кусках стало одинаковым. Каковы массы каждого из отрезанных кусков?
Ответ:
4 кг.
Более полно системы уравнений и текстовые задачи рассматриваются в соответствующих темах. Перейдем к Заданием, связанным с построением прямых и окружностей на плоскости.
• Уравнение
ах + by + с = 0,
в котором хотя бы один из коэффициентов а или b отличен от нуля, называется
уравнением прямой, а уравнение
(X - Х0)2 + (у - У0)2 = R2
— уравнением окружности с центром в точке М0(х0;
у0) и радиусом R > 0.
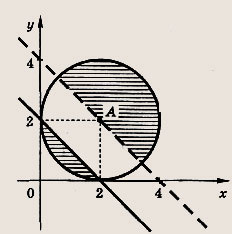
Для построения прямой нужно найти какие-либо две различные точки М1(х1; у1) и М2(х2; у2), координаты которых удовлетворяют уравнению этой прямой. Для построения окружности требуется найти ее центр и радиус (см. рис. ниже, где рассмотрены прямая у + 2х = 4 и окружность (х - 1)2 + (у - 2)2 = 5, т. е.
![]()
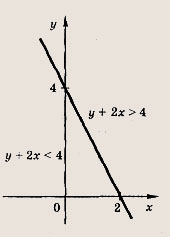
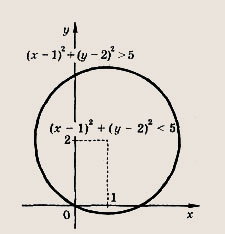
Замечание. Обе линии ах + by + с = 0 и (х - х0)2 + (у - у0)2 = R2 разбивают координатную плоскость на две части, для которых эти линии являются границей. Тогда одна из частей плоскости характеризуется тем, что координаты (х; у) всех ее точек М удовлетворяют неравенствам
ах + by + с < 0 и (х - х0)2 + (у - y0)2< R2,
а в другой части выполнены противоположные неравенства (см. рис. выше). Знак неравенства можно определить, найдя его в какой-либо одной точке соответствующей части плоскости.
Постройте графики следующих линейных функций и окружностей (38—61). На координатной плоскости отметьте штриховкой области, соответствующие указанным неравенствам (границы областей, отвечающих строгим неравенствам, условимся проводить пунктирной линией, а границы областей, отвечающих нестрогим неравенствам, — сплошной линией).
Задание 38.
![]()
Ответ:
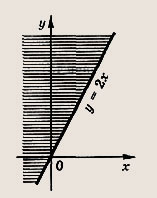
Задание 39.
у = -2х + 1, у < -2х + 1
Ответ:
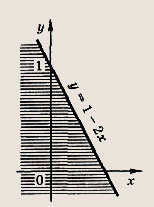
Задание 40.
![]()
Ответ:
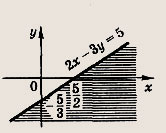
Задание 41.
![]()
Что происходит с прямой при изменении коэффициента а? Через какую точку проходят все эти прямые?
Ответ:
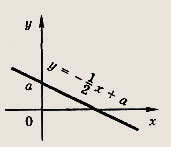
При изменении а прямая
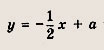
перемещается параллельно самой себе.
Задание 42.
у = ах - 1.
Что происходит с прямой при изменении коэффициента а? Через какую точку проходят все эти прямые?
Ответ:
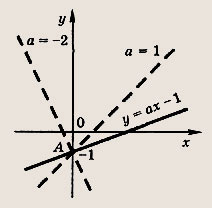
При всех а прямые у = ах - 1 проходят через точку А (0; -1). При изменении а прямая у = ах - 1 вращается вокруг точки А (0; -1).
Задание 43.
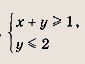
Ответ:
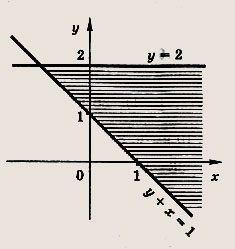
Задание 44.
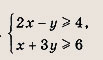
Ответ:
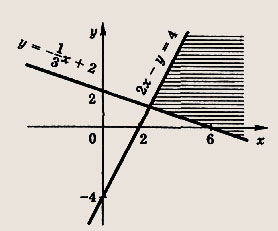
Задание 45.
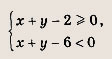
Ответ:
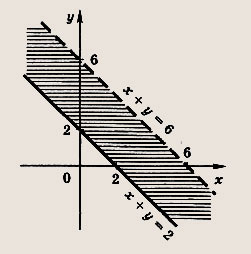
Задание 46.
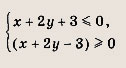
Ответ:
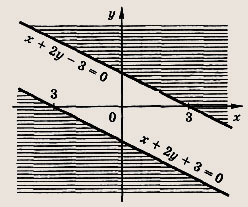
Задание 47.
(х-у)(х + 2у) > 0.
Ответ:
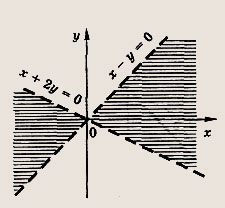
Задание 48.
![]()
Ответ:
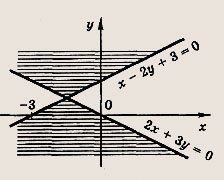
Задание 49.
![]()
Ответ:
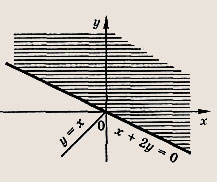
Задание 50.
(2х + у)2(х - 2у + 3) < 0
Ответ:
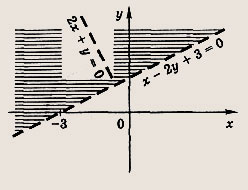
Задание 51.
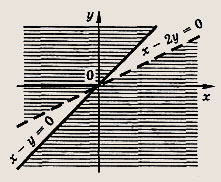
![]()
Ответ:
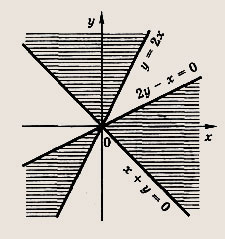
Задание 52.
![]()
Ответ:
Задание 53.
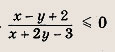
Ответ:
Задание 54.
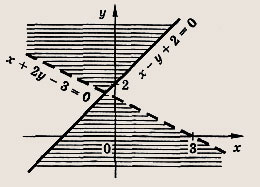
![]()
Решение:
Построим множество точек М(х; у), координаты которых удовлетворяют равенству у2 - 2ху - Зх2 = 0
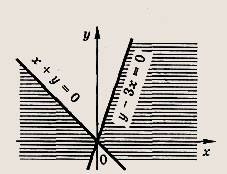
Раскладывая левую часть на множители, получаем у2 - 2ху - Зх2 = (у + х) (у - Зх) = 0. Это пара пересекающихся прямых у = -х и у = Зх. Теперь заштриховываем область
![]()
Задание 55.
х2 + ху - 2у2> 0
Ответ:
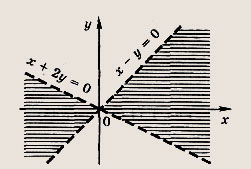
Задание 56.
![]()
Ответ:
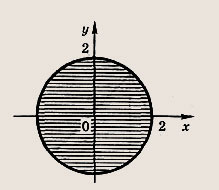
Задание 57.
![]()
Ответ:
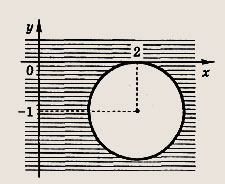
Задание 58.
![]()
Решение:
Имеем х2 - 2х + у2 + 4y = (х - 1)2 + (у + 2)2 - 5. Таким образом, равенство х2 - 2х + у2 + 4у = 0 определяет окружность
![]()
с центром в точке А(1; -2) и радиусом
![]()
Теперь заштриховываем область
![]()
Задание 59.
![]()
Ответ:
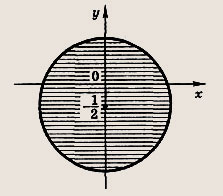
Круг с центром в точке
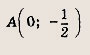
радиусом R = 2:
![]()
Задание 60.
![]()
Что происходит с заштрихованной областью при изменении коэффициента а?
Ответ:
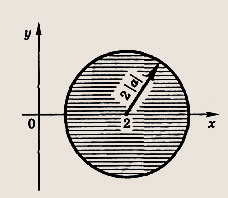
(х - 2)2 + у2 < (2|а|)2
Если а = 0, то одна точка А(2; 0). Если
![]()
то круг радиуса R = 2|а| с центром в точке А(2; 0). С увеличением |а| радиус круга увеличивается.
Задание 61.
![]()
Что происходит с заштрихованной областью при изменении коэффициента а?
Ответ:
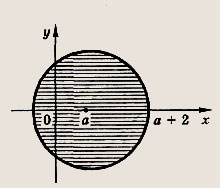
![]()
— круг радиуса R - 2 с центром в точке (а; 0). При увеличении а круг, как целое, смещается вправо.
Задание 62.
Пусть М — множество точек плоскости с координатами (х; у) таких, что числа х, у и 6 - 2х являются длинами сторон некоторого треугольника. Постройте фигуру М и найдите ее площадь.
Решение:
Для того чтобы числа х, у и (6 - 2х) являлись длинами сторон некоторого треугольника, необходимо и достаточно, чтобы эти числа были положительными и сумма любых двух из них была больше третьего числа. Получаем неравенства х > 0, у > 0, 6 - 2х > 0, х + у > 6 - 2х, 6-х>у,6-2х + у>х. Равносильная система имеет вид
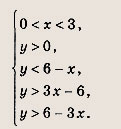
Заштриховываем соответствующую область.
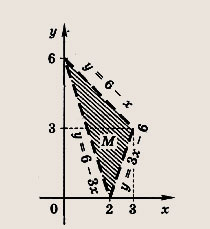
Ее площадь S = 6 кв. ед.
Задание 63.
Пусть ./V — множество точек плоскости с координатами (х; у) таких, что числа Зх, 2у и 9 - у являются длинами сторон некоторого треугольника. Постройте фигуру ./V и найдите ее площадь.
Ответ:
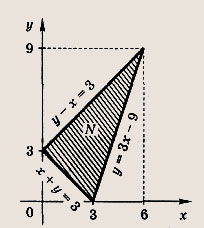
S = 18 кв. ед.
Задание 64.
Постройте множество точек, координаты которых удовлетворяют системе неравенств
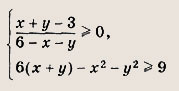
Ответ:
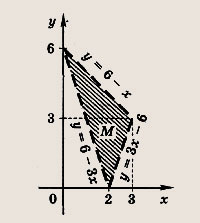
Задание 65.
Постройте множество точек, координаты которых удовлетворяют системе неравенств
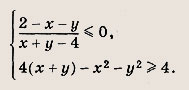
Ответ:
Задание 66.
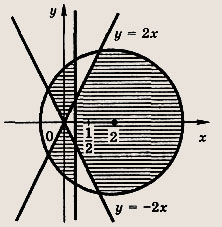
На координатной плоскости отметьте штриховкой фигуру, координаты точек которой удовлетворяют системе неравенств
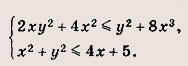
Решение:
Раскладывая на множители, перепишем первое неравенство в виде
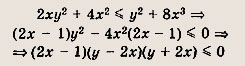
Второе неравенство принимает вид
![]()
Это круг радиуса R = 3 с центром в точке А(2; 0). Теперь заштриховываем нужную область
Задание 67.
На координатной плоскости отметьте штриховкой фигуру, координаты точек которой удовлетворяют системе неравенств
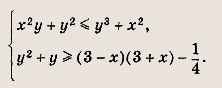
Ответ:
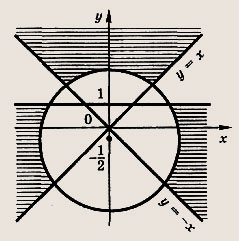
![]()
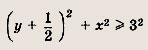
Задание 68.
При всех а укажите наименьший корень уравнения
х3 - Зах2 - (а - 1)2х + За(а - 1)2 = 0
Решение:
Раскладываем левую часть на множители: х3 - Зах2 -- (а - 1)2х + За(а - 1)2 = х2(х - За) - (а - 1)2(х - За) = (х - За)(х - а + 1) (х + а - 1) = 0. Корнями данного уравнения являются х = За; х = а - 1; х= 1 -а.
В координатной системе Оах строим графики этих функций и функции х = min (За; а — 1; 1 - а)
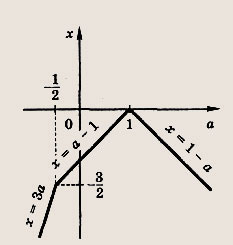
Находим точки пересечения построенных прямых и записываем ответ.
Ответ:
1)
![]()
2)
![]()
3)
![]()
Задание 69.
При всех а укажите наибольший корень ypавнения
х3 - 2ах2 - (а + 1)2х + 2а(а +1)2 = 0.
Ответ:
1)
![]()
2)
![]()
3)
![]()
Задание 70.
Решите систему неравенств
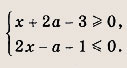
Решение:
В координатной системе Оах отметим штриховкой область, заданную указанными неравенствами
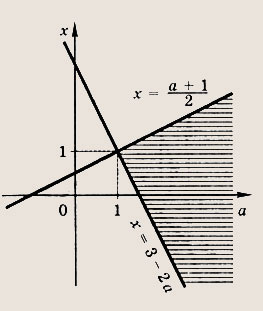
Ответ:
1)
![]()
2)
![]()
Задание 71.
Решите неравенство
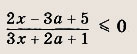
Ответ:
1)
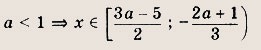
2)
![]()
Задание 72.
Найдите все а, при которых неравенство
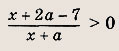
выполняется для всех
![]()
Решение:
В координатной системе Оах отметим штриховкой все точки М(а; х), координаты которых удовлетворяют указанным неравенствам (жирная штриховка выделяет те точки, у которых
![]()
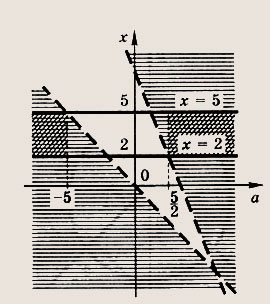
Мы видим, что только при
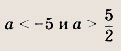
полоса
![]()
целиком лежит в заштрихованной области.
Ответ:
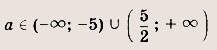
Задание 73.
Найдите все а, при которых неравенство
![]()
выполняется для всех
![]()
Ответ:
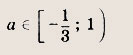
Задание 74.
При каких значениях параметра а система неравенств
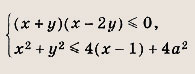
имеет хотя бы одно решение?
Решение:
Решениями данного неравенства являются все точки (х; у), лежащие внутри круга
![]()
радиуса R = = 2|а| с центром в точке A(2; 0) и в области, определяемой неравенством
![]()
Изобразим эти множества точек
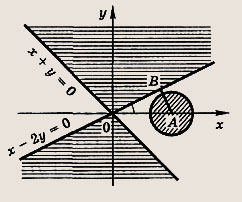
Мы видим, что система неравенств имеет решения, если радиус круга больше или равен длине перпендикуляра АВ, опущенного из точки А(2; 0) на прямую х - 2у = 0. Так как
![]()
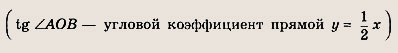
то OB = 2АВ,
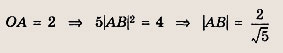
Таким образом, система имеет решения при

Ответ:
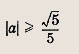
Задание 75.
При каких значениях параметра а система неравенств
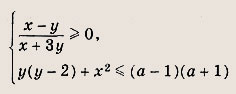
не имеет решений?
Ответ:
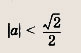
Задание 76.
Найдите все значения параметров а и b, при которых система уравнений
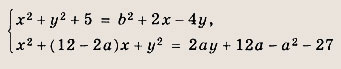
удовлетворяющие условию
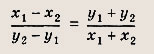
Решение:
Перепишем систему так:
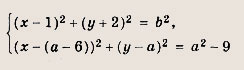
а указанное условие преобразуем к виду х12 + y12 = х22 + у22 . Таким образом, точки пересечения двух окружностей
(х - 1)2 + (у + 2)2 = |b|2 и (х-(а- 6))2 + (у - а)2 = а2 + 9
сами должны лежать на некоторой окружности с центром О(0; 0). Для этого необходимо, чтобы их центры А(1; -2), В(а - 6; а) и точка О(0; 0) лежали на одной прямой, а именно на прямой у = -2х. Отсюда получаем, что а = -2а + 12, т. е. а = 4.
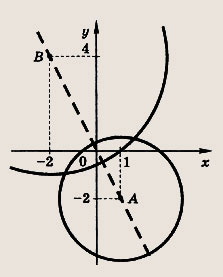
Теперь выясним, при каких |b| окружности (х- 1)2 + (y + 2)2 = |b|2 и (х + 2)2 + (y - 4)2 = 25 имеют две различные точки пересечения.
Расстояние |АВ| между центрами этих окружностей равно
![]()
Отсюда получаем, что окружности пересекаются только в том случае, если
![]()
Ответ:
![]()
Задание 77.
Найдите все значения параметров
р и д, при которых система уравнений
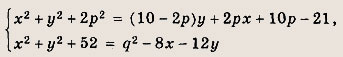
имеет два решения (х1,y1) и (х2; у2),
удовлетворяющих условию
.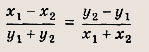
Ответ:
![]()
Задание 78.
При каких а система уравнений
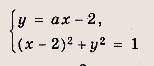
имеет единственное решение?
Ответ:
![]()
Задание 79.
При каких а система уравнений
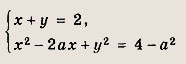
имеет решения?
Решение:
Найдем предельные положения окружностей (х - а)2 + у2 = (2)2, при которых они касаются прямой х + у = 2.
Радиус окружности равен 2, ее центр — точка (а; 0). Поэтому для предельных случаев получаем
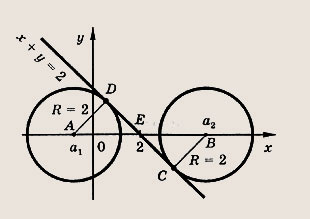
(а2 - 2)2 = 22 + 22; (2 - а1)2 = 22 + 22.
Значит, а1 и а2 — корни уравнения
а2- 4a - 4 =0,
т.е
![]()
Если
![]()
то прямая и окружность пересекаются, а, следовательно, система имеет решения.
Ответ:
![]()
Задание 80.
При каких значениях а окружность
(х - 2)2 + (у-2)2 = 1
лежит между двумя параллельными прямыми 2х + у = 2 и 2х + у =а?
Решение:
Прямая 2х + у = 2 и окружность (х - 2)2 + (у - 2)2 = 1 не пересекаются. Найдем те значения а, при которых прямая 2х + у = а является касательной к данной окружности.
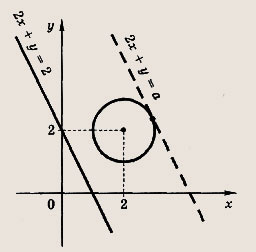
Для этого уравнение
(х - 2)2 + (а - 2 - 2х)2 = 1
должно иметь единственное решение. После раскрытия скобок приходим к квадратному уравнению
5х2 - 4(а - 1)х + а2 - 4а + 7 = 0.
Так как дискриминант квадратного трехчлена должен быть равен нулю, то получаем уравнение для вычисления коэффициента а:
![]()
Из этих двух значений следует выбрать большее, т. е.
![]()
Ответ:
![]()
