Плоская задача теории упругости
Из тела находящегося в плоском напряженном состоянии, выделена пластина, толщина которой 1 см, размеры в плане 20х20 см.
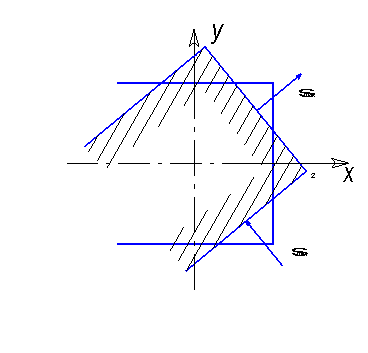
Схема закрепления пластины.
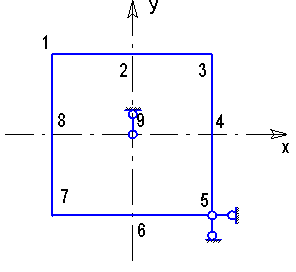
Задаваясь функцией напряжений, общий вид которой
Ф (х,у)=а 1 х 3 у+а 2 х 3 +а 3 х 2 у+а 4 х 2 +а 5 ху+а 6 у 2 +а 7 ху 2 +а 8 у 3 +а 9 ху 3
Принять два коэффициента функции согласно таблиц 1 и 2, остальные шесть коэффициентов принять равными нулю. В этих же таблицах даны значения модуля упругости Е и коэффициента Пуассона для материала пластины.
Найти общие выражения для напряжений s х , s у , t ху (объемные силы не учитывать) и построить эпюры этих напряжений для контура пластины.
Определить выражения для перемещений U и V. Показать графически(на миллиметровке) перемещение пластины в результате деформирования, определив компоненты перемещений U и V в девяти точках, указанных на схеме. Для наглядности изображения для перемещений выбрать более крупный масштаб, чем масштаб длин. Значение U и V свести в таблицу.
Расчет.
Дано : а 3 =1/3, а 4 = 1
Е=0,69*10 6 кг/см 2
n =0,33
Решение :
1.Проверим, удовлетворяет ли функция напряжений бигармоническому уравнению.
Ф(х,у)=
![]()
Поскольку производные
![]()
-бигармоническое уравнение удовлетворяется.
2.Определяем компоненты по формулам Эри, принимая объемные силы равными нулю.
s
х
=
![]()
s
у
=
![]()
t
ху
=
![]()
3.Строим эпюры напряжений для контура пластины согласно полученным аналитическим напряжениям.
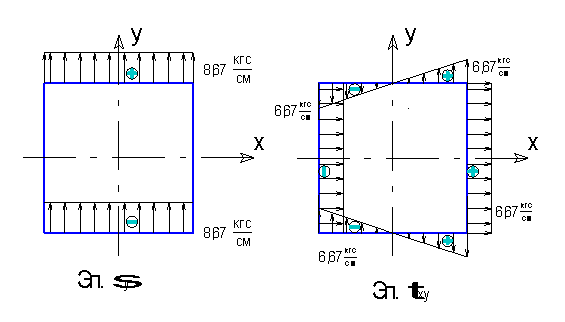
4.Проверяем равновесие пластины
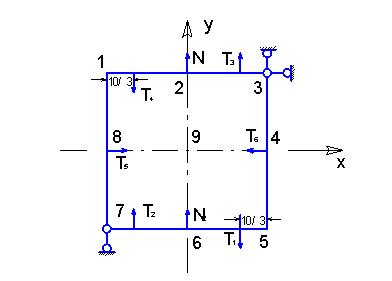
Уравненения равновесия:
S х=0 -Т 5 +Т 6 =0 > 0=0
S y=0 Т 4 +Т 3 +Т 2 -Т 1 -N 2 +N 1 =0 > 0=0
S M=0 M (T 4 T 3 )=-M(T 2 T 1 ) > 0=0
удовлетворяется, т.е. пластина находится в равновесии.
5.Для точки А с координатами (5,-5) найти величины главных напряжений и положение главных осей для точки А.
В этой точке напряжения в основных площадках. s х =0, s у =-1,33, t ху =3,33,
Найдем главное напряжение по формуле:
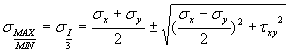 =-0,665
±
3,396 кгс/см
2
=-0,665
±
3,396 кгс/см
2
s max = s I =2,731 МПа
s min = s II = -4,061 МПа
Находим направление главных осей.
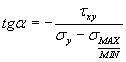
![]() a
I
=39,36
o
a
I
=39,36
o
![]() a
II
=-50,64
o
a
II
=-50,64
o
6.Определяем компоненты деформации
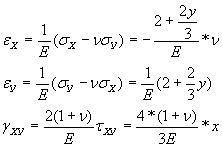
7.Находим компоненты перемещений
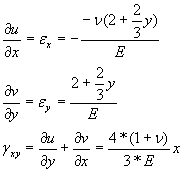
Интегрируем полученные выражения
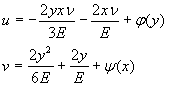
j (у), y (х) –некоторые функции интегрирования
![]()
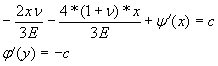
или
![]()
После интегрирования получим
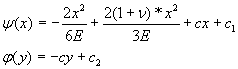
где с 1 и с 2 – постоянные интегрирования
С учетом получения выражений для j (у) и y (х) компоненты перемещений имеет вид
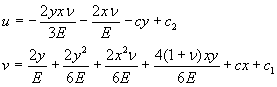
Постоянные с 1 , с 2 , и с определяем из условий закрепления пластины:
1)
![]() v =0 или
v =0 или
![]()
2) v =0 или
![]()
3) u =0 или
![]()
Окончательные выражения для функций перемещений u и v
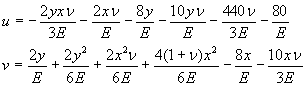
Покажем деформированное состояние пластины определив для этого перемещение в 9-ти точках.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||
|
координаты |
Х(см) |
-10 |
0 |
10 |
10 |
10 |
0 |
-10 |
-10 |
0 |
|
У(см) |
10 |
10 |
10 |
0 |
-10 |
-10 |
-10 |
0 |
0 |
|
|
V*10 -4 |
3,8 |
0,77 |
0,58 |
-0,19 |
0 |
0,19 |
3,2 |
3,1 |
0 |
|
|
U*10 -4 |
-3,1 |
-3,5 |
-3,9 |
-1,9 |
0 |
-0,23 |
-0,45 |
-1,8 |
-1,9 |
|
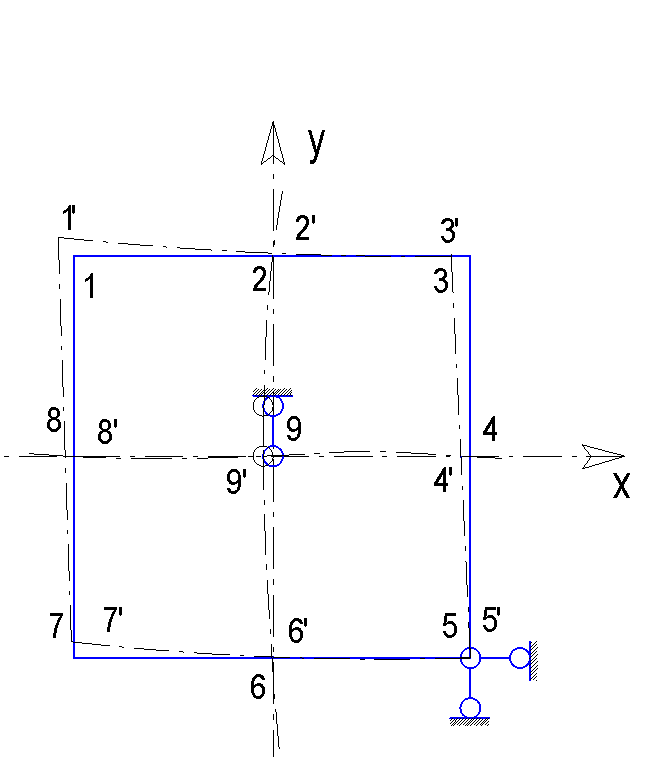
Масштаб
- длин: в 1см – 2см
- перемещений: в 1см - 1*10 -4 см
