Быков В.В. bikov@rambler.ru
Содержание
Введение…………………………………………………………………………………………3
§1. Предварительные сведения……………………………………5
§2. Основные факты………………………………………………………………8
§3. Теоремы Штурма……………………………………………………………18
Использованная литература…………………………………………27
Введение
Тема дипломной работы “Теорема Штурма”, связана с именем французского математика Жака Шарля Франсуа Штурма.
Штурм Жак Шарль Франсуа (Sturm J. Ch. F. – правильное произношение: Стюрм), родился 29 сентября 1803 года в Женеве. Был членом Парижской академии наук с 1836, а также иностранным членом – корреспондентом Петербургской академии наук с того же года. С 1840 года был профессором Политехнической школы в Париже.
Штурм (1824/25) и Раабе (1827) ввели главные формулы сферической тригонометрии при помощи пространственных координат.
Теорему Фурье ( Теорема о числе действительных корней между двумя данными пределами ), математика Жозефа Фурье (Joseph Fourier, 1768-1830), затмила более общая теорема, опубликованная Штурмом в Bull. mathem., 1829. Доказательство сам Штурм представил только в одной премированной работе 1835г. Коши Огюстен (Cauchy Augustin, 1789-1857) распространил теорему Штурма на комплексные корни (1831). Дополнение к ней дал также Сильвестр Джемс Джозеф (Sylvester Y.Y., 1814-1897) в 1839 году и позже.
Основные работы Жана Шарля Штурма относятся к решению краевых задач уравнений математической физики и связанной с этим задачей о разыскивании собственных значений и собственных функций для обыкновенных дифференциальных уравнений. (Задача Штурма-Лиувилля, о нахождении отличных от нуля решений дифференциальных уравнений :
-(p(t)u ¢ ) ¢ +q(t)u= l u,
удовлетворяющих граничным условиям вида:
А 1 u(a)+B 1 u ¢ (a)=0,
A 2 u(b)+B 2 u ¢ (b)=0,
(так называемых собственных функций), а также о нахождении значений параметра l (собственных значений), при которых существуют такие решения. При некоторых условиях на коэффициенты p(t), q(t) задача Штурма-Лиувилля сводилась к рассмотрению аналогичной задачи для уравнения вида: -u ¢ ¢ +q(x)u= l u).
Эта задача была впервые исследована Штурмом и Жозефом Лиувиллем (Joseph Liouville, 1809-1882) в 1837г. и закончена в 1841 г.
Также Жак Штурм дал общий метод для определения числа корней алгебраических уравнений, лежащих на заданном отрезке, названный правилом Штурма, который позволяет находить непересекающиеся интервалы, содержащие каждый по одному действительному корню данного алгебраического многочлена с действительными коэффициентами (уже упоминалось выше).
Ему принадлежат ряд работ по оптике и механике.
Штурм Жак Шарль Франсуа умер 18 декабря 1855года.
§ 1. Предварительные сведения
Среди дифференциальных уравнений, наиболее часто используемых в математике и физике, следует выделить линейное уравнение второго порядка, имеющее вид
u"+ g(t)u' + f(t)u=h(t)
(1.1)или
(р (t) и')' + q (f) и
= h(t) . (1.2)Как правило, если не оговорено противное, предполагается, что функции (t), g (f), h (f) и р (f) № 0, q (t), входящие в эти уравнения, являются непрерывными (вещественными или комплексными) на некотором t -интервале J , который может быть как ограниченным, так и неограниченным. Причина, по которой предполагается, что р(t) № 0, скоро станет ясной.
Из двух выражений (1.1) и (1.2) последнее является более общим, поскольку уравнение (1.1) может быть записано в виде
(p(t) и')' + р(t) f(t)u= р (t) h (t),
(1.3)если определить p(t) следующим образом:
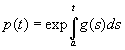 (1.4)
(1.4)
при некотором a€J . Частичное обращение этого утверждения также верно, поскольку если функция
р(t) непрерывно дифференцируема, уравнение (1.2) можно записать в виде
![]() ,
,
а это уравнение имеет вид (1.1).
В случае, если функция
р (t)
непрерывна, но не имеет непрерывной производной, уравнение (1.2) не может быть записано в виде (1.1). Тогда уравнение (1.2) можно интерпретировать как линейную систему из двух уравнений первого порядка для неизвестного двумерного вектора
![]() :
:
![]() ,
,
![]() . (1.5)
. (1.5)
Другими словами, решение и = и (t) уравнения (1.2) должно быть такой непрерывно дифференцируемой функцией, что функция р(t) u'(t) имеет непрерывную производную, удовлетворяющую (1.2). Если р(t) № 0 и q(t), h(t) непрерывны, к системе (1.5) , а потому и к уравнению (1.2) применимы стандартные теоремы существования и единственности для линейных систем (Мы можем рассматривать также более общие (т. е. менее гладкие) типы решений, если предполагать, например, только, что функции 1/ p(t), q (t), h (t) локально интегрируемы.)
Частному случаю уравнения
(1.2)
при
![]() соответствует уравнение
соответствует уравнение
и" + q(t) u = h(t).
(1.6)
Если функция
![]() принимает вещественные значения, уравнение
(1.2)
может быть приведено к такому виду с помощью замены независимых переменных
принимает вещественные значения, уравнение
(1.2)
может быть приведено к такому виду с помощью замены независимых переменных
![]() , т.е.
, т.е.
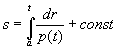 (1.7)
(1.7)
при некотором
a € J.
Функция
s = s
(t)
имеет производную
![]() и потому строго монотонна. Следовательно, функция
s = s (
t)
имеет обратную
t= t (s),
определенную на некотором
s
-интервале. После введения новой независимой
переменной s уравнение
(1.2)
переходит в уравнение
и потому строго монотонна. Следовательно, функция
s = s (
t)
имеет обратную
t= t (s),
определенную на некотором
s
-интервале. После введения новой независимой
переменной s уравнение
(1.2)
переходит в уравнение
![]()
где аргумент t выражений p(f)q(t) и p(t) h(f ) должен быть заменен функцией t = t(s). Уравнение (1.8) является уравнением типа (1.6).
Если функция g (t) имеет непрерывную производную, то уравнение (1.1) может быть приведено к виду (1.6) с помощью замены неизвестной функции и на z :
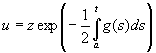 (1.9)
(1.9)
при некотором a € J . В самом деле, подстановка (1.9) в (1.1) приводит к уравнению
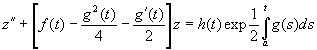 (1.10)
(1.10)
которое имеет вид (1.6).
В силу сказанного выше, мы можем считать, что рассматриваемые уравнения второго порядка в общем случае имеют вид (1.2) или (1.6). Утверждения, содержащиеся в следующих упражнениях, будут часто использоваться в дальнейшем.
§ 2. Основные факты
Прежде чем перейти к рассмотрению специальных вопросов, мы получим следствия, касающиеся однородного и неоднородного уравнений
![]()
![]()
Для этого перепишем скалярные уравнения (2.1) или (2.2) в виде системы двух уравнений
![]()
![]()
где векторы
х= (х
1
, х
2
), у == (у
1
,
y
2
)
совпадают с векторами
![]() ,
,
![]() ,
A(t)-
матрица второго порядка
:
,
A(t)-
матрица второго порядка
:
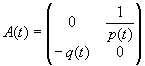
Если не оговорено противное, то предполагается, что
![]() ,
q (t), h (t)
и другие коэффициенты являются непрерывными комплексными функциями на
t
-интервале
J
(который может быть замкнутым или незамкнутым, ограниченным или неограниченным).
,
q (t), h (t)
и другие коэффициенты являются непрерывными комплексными функциями на
t
-интервале
J
(который может быть замкнутым или незамкнутым, ограниченным или неограниченным).
(i)
Если
![]() ,
,
![]() (2.6)
(2.6)
имеет единственное решение, существующее при всех
![]()
![]() ,
см. лемму IV. 1.1.
,
см. лемму IV. 1.1.
(ii)
В частном случае (2.1) уравнения (2.2) и при
(iii)
Принцип суперпозиции.
Если
![]() ,
,
![]() -
решения уравнения
(2.1), a
-
решения уравнения
(2.1), a
![]() ,
,
![]() -
постоянные, то функция
-
постоянные, то функция
![]() является решением уравнения
(2.1).
Если
является решением уравнения
(2.1).
Если
![]() -
решение уравнения
(2.2),
то функция
-
решение уравнения
(2.2),
то функция
![]() также является решением уравнения
(2.2)
тогда и только тогда, когда функция
также является решением уравнения
(2.2)
тогда и только тогда, когда функция
![]() удовлетворяет уравнению
(2.1).
удовлетворяет уравнению
(2.1).
(iv)
Если
![]() ,
,
![]() -
решения уравнения
(2.1),
то соответствующие векторные решения системы
(2.3)
-
решения уравнения
(2.1),
то соответствующие векторные решения системы
(2.3)
![]() ,
,
![]() линейно независимы (в каждой точке
t
) тогда и только тогда, когда функции
линейно независимы (в каждой точке
t
) тогда и только тогда, когда функции
![]() ,
,
![]() линейно
линейно
независимы в том смысле, что равенство
![]() ,
где
,
где
![]() и
и
![]() -
постоянные, влечет за собой
-
постоянные, влечет за собой
![]() .
.
(v)
Если
![]() ,
,
![]() -
решения уравнения
(2.1),
то существует постоянная
с,
зависящая от
и (t)
и
v (t)
и такая, что для их вронскиана
W (t) = W (t; и, v)
выполняется тождество
-
решения уравнения
(2.1),
то существует постоянная
с,
зависящая от
и (t)
и
v (t)
и такая, что для их вронскиана
W (t) = W (t; и, v)
выполняется тождество
![]() .
(2.7)
.
(2.7)
Поскольку матричным решением системы (2.3) является
![]()
det X(t)=p(t)W(t) и trA( t )=0.
(vi) Тождество Лагранжа. Рассмотрим пару уравнений
![]() ,
,
![]() ,
(2.8)
,
(2.8)
где f=f(t), g = g (t) - непрерывные функции на J. Если умножить второе уравнение на и, первое-на v и результаты вычесть, мы получим, что
![]() , (2.9)
, (2.9)
так как
![]() .
Соотношение
(2.9)
называется
тождеством Лагранжа.
Его интегральная форма
.
Соотношение
(2.9)
называется
тождеством Лагранжа.
Его интегральная форма
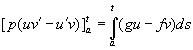 (2.10)
(2.10)
где
![]() ,
называется
формулой Грина.
,
называется
формулой Грина.
(vii)
В частности, из (v) следует, что и(t) и v(t) - линейно независимые решения уравнения (2.1) тогда и только тогда, когда в (2.7)(viii)
Если(ix)
В соответствии с результатами общей теории, в случае, когда известно одно решение
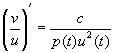 , (2.11)
, (2.11)
а после интегрирования мы будем иметь
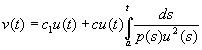 , (2.12)
, (2.12)
где
а,
![]() .
Легко проверить, что если
.
Легко проверить, что если
![]() ,
,
![]() -
произвольные постоянные и
а,
-
произвольные постоянные и
а,
![]() ,
,
(х)
Пусть
и(t), v(t)
- решения уравнения
(2.1),
удовлетворяющие
(2.7) с
![]() .
При фиксированном
.
При фиксированном
![]() решением уравнения
(2.1),
удовлетворяющим начальным условиям
и
(s) = 0,
p(s)u'(s)
=
1,
является
решением уравнения
(2.1),
удовлетворяющим начальным условиям
и
(s) = 0,
p(s)u'(s)
=
1,
является
![]() .
Поэтому решением уравнения
(2.2),
удовлетворяющим условиям
.
Поэтому решением уравнения
(2.2),
удовлетворяющим условиям
![]() ,
служит функция
,
служит функция
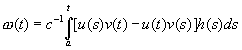 ; (2.13)
; (2.13)
(проще проверить это непосредственно). Общее решение уравнения
(2.2)
получается прибавлением к
(2.13)
общего решения
![]() уравнения
(2.1),
что дает
уравнения
(2.1),
что дает
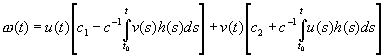 . (2.14)
. (2.14)
Если замкнутый ограниченный интервал [a,b] содержится в J , то, полагая
![]() ,
,
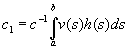 ,
,
![]()
мы получаем из (2.14) частное решение
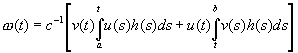
Оно может быть записано в виде
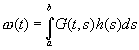
где
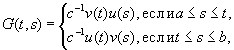
матрица С (t) зависит от
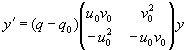
(xii)
Если известно частное решение
![]() уравнения
(2.27),
не равное нулю на
J
,
то мы можем определить линейно независимые решения с помощью квадратур
(см. (ix))
и затем найти матрицу, входящую в
(2.28).
В действительности, тот же результат можно получить более прямым путем. Пусть уравнение
(2.27)
имеет решение
уравнения
(2.27),
не равное нулю на
J
,
то мы можем определить линейно независимые решения с помощью квадратур
(см. (ix))
и затем найти матрицу, входящую в
(2.28).
В действительности, тот же результат можно получить более прямым путем. Пусть уравнение
(2.27)
имеет решение
![]() на интервале
J
.
Заменим неизвестную функцию
и
в
(2.1)
на
z
, так что
на интервале
J
.
Заменим неизвестную функцию
и
в
(2.1)
на
z
, так что
![]() .
(2.29)
.
(2.29)
Функция z удовлетворяет дифференциальному уравнению
![]() .
.
Умножая его на
![]() ,
мы получаем, что
,
мы получаем, что
![]() (2.30)
(2.30)
или, в силу (2.27) , что
![]() , (2.31)
, (2.31)
т. е. подстановка
(2.29)
приводит уравнение
(2.1)
к
(2.30)
или к
(2.31
). Мы могли также начинать не с решения
![]() дифференциального уравнения
(2.27)
, а с функции
дифференциального уравнения
(2.27)
, а с функции
![]() ,
имеющей непрерывную производную
,
имеющей непрерывную производную
![]() и такой, что
и такой, что
![]() непрерывно дифференцируема.
При этом
непрерывно дифференцируема.
При этом
![]() определяется равенством
(2.27)
, так что
определяется равенством
(2.27)
, так что
![]() .
Подстановка
(2.29)
будет называться также
вариацией постоянных.
.
Подстановка
(2.29)
будет называться также
вариацией постоянных.
(xiii)
Подстановка Лиувилля. В качестве частного случая рассмотрим (2.1) с р (t) = 1:и" + q (t) и = 0. (2.32)
Предположим, что функция q (t) имеет непрерывную производную второго порядка, вещественна и не равна нулю, так что
±q (t)
> 0, где ± = sgn q (t) (2.33)не зависит от t. Рассмотрим вариацию постоянных
![]() . (2.34)
. (2.34)
Тогда
(2.32)
сводится к
(2.30),
где
![]() , т. е. к уравнению
, т. е. к уравнению
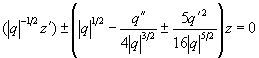 (2.35)
(2.35)
Замена независимых переменных
![]() ,
определенная соотношением
,
определенная соотношением
![]() , (2.36)
, (2.36)
переводит (2.35) в уравнение
![]() (2.37)
(2.37)
где
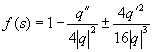 (2.38)
(2.38)
а аргументом функции q и ее производных служит функция t = t (s), обратная к функции s = s ( f), определяемой из (2.36) с помощью квадратуры; см. (1.7). В этих формулах штрих означает дифференцирование по t , так что q' = dqldt.
Замена переменных (2.34), (2.36) называется подстановкой Лиувилля. Эта подстановка, или повторное применение ее, часто приводит к дифференциальному уравнению типа (2.37), в котором функция f (s) “близка” к постоянной . Простой предельный случай такой подстановки см. в упр. 1.1(с).
(xiv)
Уравнения Риккати. В п. (xi), (xii) и (xiii) рассматривались преобразования уравнения (2.1) в различные линейные уравнения второго порядка или в соответствующие линейные системы двух уравнений первого порядка. Иногда удобно преобразовать (2.1) в соответствующее нелинейное уравнение или систему. Для этого чаще всего используется следующий метод. Пусть
![]() , (2.39)
, (2.39)
так что
![]() .
Тогда после деления
(2.1)
на
и
результат можно записать в виде
.
Тогда после деления
(2.1)
на
и
результат можно записать в виде
![]() . (2.40)
. (2.40)
Это уравнение называется уравнением
Риккати
, соответствующим
(2.1).
(В общем случае уравнение вида
![]() ,
где правая часть является квадратичным полиномом от
г,
называется
дифференциальным уравнением Риккати.)
,
где правая часть является квадратичным полиномом от
г,
называется
дифференциальным уравнением Риккати.)
Читателю предоставляется проверка того факта, что если
и (t) -
решение уравнения
(2.1),
не равное нулю на
t
- интервале
![]() ,
то функция
(2.39)
является решением уравнения
(2.40)
на
J';
,
то функция
(2.39)
является решением уравнения
(2.40)
на
J';
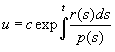 (2.41)
(2.41)
уравнения (2.1), не равное нулю ни в одной точке из J'.
(xv)
Преобразование Прюфера.
В случае, когда уравнение
(2.1)
имеет вещественные коэффициенты, часто используется следующее преобразование
.
Пусть
![]() -вещественное решение уравнения 2.1, и пусть
-вещественное решение уравнения 2.1, и пусть
![]() .
.
Поскольку
и
и
и'
не могут обратиться в нуль одновременно, то, фиксируя соответствующее значение функции
![]() в некоторой точке
в некоторой точке
![]() ,
мы определяем с помощью второго из равенств
(2.42)
непрерывно дифференцируемую функцию
,
мы определяем с помощью второго из равенств
(2.42)
непрерывно дифференцируемую функцию
![]() .
Соотношения
(2.42)
переводят уравнение
(2.1)
в систему
.
Соотношения
(2.42)
переводят уравнение
(2.1)
в систему
![]()
![]() (2.44)
(2.44)
В уравнение
(2.43)
входит лишь одна из неизвестных функций
![]() .
Если решение
.
Если решение
![]() уравнения
(2.43)
известно, то соответствующее решение уравнения
(2.44)
может быть найдено с помощью квадратуры.
уравнения
(2.43)
известно, то соответствующее решение уравнения
(2.44)
может быть найдено с помощью квадратуры.
Преимущество уравнения (2.43) по сравнению с (2.40) состоит в том, что всякое решение уравнения (2.43) существует на всем интервале J , где непрерывны р и q. Это видно из соотношения, связывающего решения уравнений (2.1) и (2.43).
Упражнение 2.1
.
Проверьте, что если функция
![]() непрерывна на
J
и имеет локально ограниченную вариацию (т. е. имеет ограниченную вариацию на всех замкнутых ограниченных подин-тервалах из
J
)
и если
- вещественное решение уравнения
(2.1),
то равенства
непрерывна на
J
и имеет локально ограниченную вариацию (т. е. имеет ограниченную вариацию на всех замкнутых ограниченных подин-тервалах из
J
)
и если
- вещественное решение уравнения
(2.1),
то равенства
![]()
при фиксированном значении
![]() для некоторого
для некоторого
![]() однозначно определяют непрерывные функции
однозначно определяют непрерывные функции
![]() ,
имеющие локально ограниченную вариацию и
,
имеющие локально ограниченную вариацию и
![]()
Соотношения
(2.46)
и
(2.47)
следует понимать так, что интегралы Римана - Стильтьеса от обеих их частей равны. Обратно, (непрерывные) решения системы уравнений
(2.46), (2.47)
определяют решения уравнения
(2.1)
с помощью соотношений
(2.45).
Заметим, что если
q (t)
> 0,
р (t)
> 0
и функция
q(t) р
(
t
)
имеет локально ограниченную вариацию, то, полагая
![]() , мы получаем
q/
, мы получаем
q/
![]()
![]()
![]()
![]()
![]()
§ 3 .
Теоремы Штурма
В этом параграфе мы будем рассматривать только уравнение вида (2.1) с вещественными непрерывными коэффициентами
р (t)
> 0,
q (t).
Под “решением” мы будем понимать “вещественное, нетривиальное (т. е.
![]() ) решение”. Нас будет интересовать множество нулей решения
u (t)
.
Для изучения этих нулей часто оказывается полезным преобразование Прюфера (2.42), поскольку
) решение”. Нас будет интересовать множество нулей решения
u (t)
.
Для изучения этих нулей часто оказывается полезным преобразование Прюфера (2.42), поскольку
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() .
.
Лемма 3.1.
Пусть
![]() - вещественное решение уравнения
(2.1)
при
- вещественное решение уравнения
(2.1)
при
![]() , где
, где
![]() и
и
![]() вещественны и непрерывны. Пусть функция
и (t)
имеет в точности
вещественны и непрерывны. Пусть функция
и (t)
имеет в точности
![]() нулей
нулей
![]() при
при
![]() . Предположим, что
. Предположим, что
![]() - непрерывная функция, определенная равенством
(2.42),
и
- непрерывная функция, определенная равенством
(2.42),
и
![]() .
Тогда
.
Тогда
![]() и
и
![]() при
при
![]() .
.
Доказательство.
Заметим, что в той точке
t
,
где
u=0
, т. е. где
![]() , производная
, производная
![]() в силу (2.43). Следовательно, функция
в силу (2.43). Следовательно, функция
![]() возрастает в окрестности точек, где
возрастает в окрестности точек, где
![]() для некоторого целого
j
. Отсюда следует, что если
для некоторого целого
j
. Отсюда следует, что если
![]() и
и
![]() , то
, то
![]() при
при
![]() , а также что если
, а также что если
![]() , то
, то
![]() при
при
![]() . Тем самым лемма доказана.
. Тем самым лемма доказана.
В теоремах этого параграфа будут рассматриваться два уравнения
![]()
где функции
![]() вещественны и непрерывны на интервале
J
.
и
вещественны и непрерывны на интервале
J
.
и
![]()
В этом случае уравнение (3.1) называется мажорантой Штурма для (3.1) на J , а уравнение (3.1) -минорантой Штурма для (3.1). Если дополнительно известно, что соотношения
![]()
или
![]()
выполняются в некоторой точке
![]() ,
то уравнение
,
то уравнение
Теорема 3.1
(первая теорема сравнения Штурма).
Пусть коэффициенты уравнения
![]() непрерывны на интервале J:
непрерывны на интервале J:
![]() , и пусть уравнение
(3.3
2
)
является мажорантой Штурма для
(3.1
1
)
.
Предположим, что функция
, и пусть уравнение
(3.3
2
)
является мажорантой Штурма для
(3.1
1
)
.
Предположим, что функция
![]() является решением уравнения
(3.1
1
)
и имеет точно
является решением уравнения
(3.1
1
)
и имеет точно
![]() нулей
нулей
![]() при
при
![]() ,а функция
,а функция
![]() удовлетворяет уравнению
(3.1
2
)
и
удовлетворяет уравнению
(3.1
2
)
и
![]()
при
Доказательство.
В силу (3.4) можно определить при
![]() пару непрерывных функций
пару непрерывных функций
![]() с помощью соотношений
с помощью соотношений
![]()
Тогда справедливы аналоги соотношения (2.43):
![]()
Поскольку непрерывные функции
![]() , гладким образом зависят от
, гладким образом зависят от
![]() , решения системы (3.6) однозначно определяются своими начальными условиями. Из (3.2) следует, что
, решения системы (3.6) однозначно определяются своими начальными условиями. Из (3.2) следует, что
![]() при
при
![]() и всех
и всех
![]() . Поэтому последняя часть (3.5) и следствие III.4.2 означают, что
. Поэтому последняя часть (3.5) и следствие III.4.2 означают, что
![]()
Чтобы доказать последнюю часть теоремы, предположим вначале, что при
![]() в (3.4) имеет место строгое неравенство. Тогда
в (3.4) имеет место строгое неравенство. Тогда
![]() . Обозначим через
. Обозначим через
![]() решение уравнения
(3.6
2
)
, удовлетворяющее начальному условию
решение уравнения
(3.6
2
)
, удовлетворяющее начальному условию
![]() , так что
, так что
![]() . Поскольку решение уравнения
(3.6
2
)
однозначно определяется начальными условиями,
. Поскольку решение уравнения
(3.6
2
)
однозначно определяется начальными условиями,
![]() при
при
![]() . Неравенство, аналогичное (3.7), означает, что
. Неравенство, аналогичное (3.7), означает, что
![]() потому
потому
![]() . Следовательно,
. Следовательно,
![]() имеет n нулей при
имеет n нулей при
![]() .
.
Рассмотрим теперь тот случай, когда в (3.4) имеет место равенство, но в некоторой точке из
![]() выполняется либо
(3.3
1
)
, либо
(3.3
2
)
. Запишем
(3.6
2
)
в виде
выполняется либо
(3.3
1
)
, либо
(3.3
2
)
. Запишем
(3.6
2
)
в виде
![]()
где
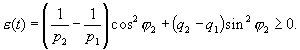
Если доказываемое утверждение неверно, то из уже рассмотренного случая следует, что
![]() при
при
![]() .Поэтому
.Поэтому
![]() и
и
![]() при
при
![]() .
Так как
.
Так как
Следовательно, если
![]() при некотором
t
,
то
при некотором
t
,
то
![]() , т. е.
, т. е.
![]() . Если
(3.3
1
)
не выполняется ни при каком
t
из отрезка
. Если
(3.3
1
)
не выполняется ни при каком
t
из отрезка
![]() ,
то при некотором
t
имеет место
(3.3
2
)
, и потому
(3.3
2
)
справедливо на некотором подинтервале из
,
то при некотором
t
имеет место
(3.3
2
)
, и потому
(3.3
2
)
справедливо на некотором подинтервале из
![]() . Но тогда на этом интервале
. Но тогда на этом интервале
![]() и потому
и потому
![]() .
Однако это противоречит условию
.
Однако это противоречит условию
![]() .
Доказательство закончено.
.
Доказательство закончено.
Следствие
3.1 (теорема Штурма о разделении нулей).
Пусть уравнение
(3.1
2
)
является мажорантой Штурма для
(3.1
1
)
на интервале J, и пусть
![]() -
вещественные решения уравнений,
(3.3
j
)
.
Пусть
-
вещественные решения уравнений,
(3.3
j
)
.
Пусть
![]() обращается в нуль в двух точках
обращается в нуль в двух точках
![]() интервала J. Тогда
интервала J. Тогда
![]() имеет по крайней мере один нуль на
имеет по крайней мере один нуль на
![]() . В частности, если
. В частности, если
![]() и
и
![]() вещественные линейно независимые решения уравнения
(3.1
1
)
вещественные линейно независимые решения уравнения
(3.1
1
)
![]() (3.1
2
)
.
То нули функции
(3.1
2
)
.
То нули функции
![]() разделяют нули функции
разделяют нули функции
![]() и разделяются ими.
и разделяются ими.
Заметим, что, последнее утверждение этой теоремы имеет смысл, поскольку нули функций
![]() и
и
![]() не имеют на
J
предельных точек. Кроме того,
не имеют на
J
предельных точек. Кроме того,
![]() ,
,
![]() не могут иметь общего нуля
не могут иметь общего нуля
![]() ,
так как в противном случае в силу того, что решения уравнения
(3.1
1
)
единственны,
,
так как в противном случае в силу того, что решения уравнения
(3.1
1
)
единственны,
![]() , где
, где
![]() (так что
(так что
![]() и
и
![]() не являются линейно независимыми).
не являются линейно независимыми).
Упражнение 3.1 . (Другое доказательство теоремы Штурма о разделении нулей, когда p 1 (t) º p 2 (t)>0, q 2 (t) ³ q 1 (t).)
Предположим, что u 1 (t)>0 при t 1 <t 2 <t 3 и утверждение неверно: например, u 2 (t)>0 при t 1 £ t £ t 2 . Умножая (p 1 (t)u ¢ ) ¢ +q 1 (t)u=0, где u=u 1 , на u 2 , а (p 2 (t)u ¢ ) ¢ +q 2 (t)u=0, где u=u 2 , на u 1 , вычитая и интегрируя по [t 1, t 2 ], получаем:
p(t)(u 1 ¢ u 2 -u 1 u 2 ¢ ) ³ 0, при t 1 £ t £ t 2 , где p=p 1 =p 2 . Это означает, что (u 1 /u 2 ) ¢ ³ 0; поэтому u 1 /u 2 >0 при t 1 <t £ t 2 , т.е. получается, что u 1 (t 2 )>0 чего быть не может.
Решение:
(p 1 (t)u ¢ ) ¢ +q 1 (t)u=0, u=u 1
(p 1 (t)u 1 ¢ ) ¢ +q 1 (t)u 1 =0.
Умножим левую часть равенства на u 2 , получим:
u 2 (p 1 (t)u 1 ¢ ) ¢ +q 1 (t)u 1 u 2 =0.
Во втором уравнении проделаем соответствующие операции:
(p 2 (t)u ¢ ) ¢ +q 2 (t)u=0, u 2 =u
(p 2 (t)u 2 ¢ ) ¢ +q 2 (t)u 2 =0.
Умножим левую часть равенства на u 1 , получим:
u 1 (p 2 (t)u 2 ¢ ) ¢ +q 2 (t)u 1 u 2 =0.
Вычитаем из первого уравнения второе, получим:
u 2 (p 1 u 1 ¢ ) ¢ +q 1 u 1 u 2 -u 1 (p 2 u 2 ¢ ) ¢ -q 2 u 1 u 2 =0, p=p 1 =p 2
u 2 (pu 1 ¢ ) ¢ +q 1 u 1 u 2 -u 1 (pu 2 ¢ ) ¢ -q 2 u 1 u 2 =0
(u 2 (pu 1 ¢ ) ¢ -u 1 (pu 2 ¢ ) ¢ )+u 1 u 2 (q 1 -q 2 )=0
Упростим это уравнение,
u 2 (p ¢ u 1 ¢ +pu 1 ¢ ¢ )-u 1 (p ¢ u 2 ¢ +pu 2 ¢ ¢ )+u 1 u 2 (q 1 -q 2 )=0
Раскроем скобки, получим:
p ¢ u 1 ¢ u 2 + pu 1 ¢ ¢ u 2 - p ¢ u 1 u 2 ¢ -pu 1 u 2 ¢ ¢ +u 1 u 2 (q 1 -q 2 )=0.
Сравнивая с формулой (2.2), получаем:
(p(u 1 ¢ u 2 -u 1 u 2 ¢ )) ¢ +u 1 u 2 (q 1 -q 2 )=0
(p(u 1 ¢ u 2 -u 1 u 2 ¢ )) ¢ -u 1 u 2 (q 2 -q 1 )=0
(p(u 1 ¢ u 2 -u 1 u 2 ¢ )) ¢ =u 1 u 2 (q 2 -q 1 )=0.
Проинтегрируем это уравнение по [t 1 ,t], получим:
![]() [p(u
1
¢
u
2
-u
2
¢
u
1
)]
¢
dt =
[p(u
1
¢
u
2
-u
2
¢
u
1
)]
¢
dt =
![]() u
1
u
2
(q
2
-q
1
)dt, где
u
1
u
2
(q
2
-q
1
)dt, где
u 1 u 2 >0, q 2 -q 1 ³ 0. Значит p(u 1 ¢ u 2 -u 1 u 2 ¢ ) ³ 0.
Т.о. (u 1 /u 2 ) ¢ ³ 0 Þ u 1 /u 2 >0.
Упражнение 3.2.
с) Проверьте, что вещественные решения u(t)
¹
0 уравнения u
¢
¢
+
m
/t
2
u=0 (1/17) имеет не более одного нуля при t>0, если
m
£
![]() , и эти решения имеют бесконечно много нулей при t>0, если
m
>
, и эти решения имеют бесконечно много нулей при t>0, если
m
>
![]() . В последнем случае множество нулей имеет две предельные точки t=0 и t=
¥
.
. В последнем случае множество нулей имеет две предельные точки t=0 и t=
¥
.
Решение: в §1 было рассмотрено упражнение 1.1 с), где показали, что функция u=t
l
является решением уравнения u
¢
¢
+
m
/t
2
u=0 тогда и только тогда, когда
l
удовлетворяет уравнению
l
(
l
-1)+
m
=0. Решая его получили :
l
=
![]() ±
±
![]() m
.
m
.
Если m >1/4, то корни l 1 и l 2 – комплексные, т.е.
u=t
1/2
[cos (
![]() m
-1/4 ln t)c
1
+c
2
sin(
m
-1/4 ln t)c
1
+c
2
sin(
![]() m
-1/4 ln t)]
m
-1/4 ln t)]
имеют бесчисленное множество нулей. В частности, если положить:
c 1 =sinu ,c 2 =cosu,
то получим:
u= t
1/2
[sin u cos (
![]() m
-1/4 ln t)+cos u sin (
m
-1/4 ln t)+cos u sin (
![]() m
-1/4 ln t)]=
m
-1/4 ln t)]=
t
1/2
[sin (u+
![]() m
-1/4 ln t)].
m
-1/4 ln t)].
Если m <1/4, то решение
u=с 1 t 1/2+ +c 2 t 1/2-
имеют не более одного нуля.
Так же, если m =1/4, то решение
u=c 1 t 1/2 +c 2 t 1/2 ln t
имеют не более одного нуля.
d) Рассмотрим уравнение Бесселя:
v ¢ ¢ +v ¢ /t+(1- m 2 /t 2 )v=0, (3.10)
где m -вещественный параметр. Вариация постоянных u=t 1/2 /v переводит уравнение (3.10) в уравнение:
u ¢ ¢ +(1- a /t 2 )u=0, где a = m 2 -1/4 (3.11)
Проверим истинность этого утверждения u=t 1/2 v, следовательно:
v=u/t 1/2 =ut -1/2.
Найдём первую производную:
v ¢ =(ut -1/2 ) ¢ =u ¢ t -1/2 +u(t -1/2 ) ¢ =u ¢ t -1/2 -1/2ut -3/2 .
Теперь вторую производную:
v ¢ ¢ =(u ¢ t 1/2 ) ¢ -1/2(ut -3/2 ) ¢ =u ¢ ¢ t -1/2 +u ¢ (t -1/2 ) ¢ -1/2(u ¢ t -3/2 +u(t -3/2 ) ¢ )=
=u ¢ ¢ t -1/2 –1/2u ¢ t -3/2 -1/2u ¢ t -3/2 +3/4uut -5/2 =
=u ¢ ¢ t -1/2 -u ¢ t -3/2 +3/4ut -5/2 .
Подставляя в уравнение (3.10), получим:
v ¢ ¢ +v ¢ /t+(1- m 2 /t 2 )v=0.
u ¢ ¢ t -1/2 -u ¢ t -3/2 +3/4ut -5/2 +1/t(u ¢ t -1/2 -1/2ut -3/2 )+(1- m 2 /t 2 )ut -1/2 =0
t -1/2 (u ¢ ¢ -u ¢ t -1 +3/4ut -2 +u ¢ t -1 -1/2ut -2 +u(1- m 2 /t 2 ))=0
u ¢ ¢ +1/4ut -2 +u(1- m 2 /t 2 )=0
u ¢ ¢ +u- m 2 u/t 2 +1/4ut -2 =0
u ¢ ¢ +u-( m 2 u-1/4u)/t 2 =0
u ¢ ¢ +u-(( m 2 -1/4)u)/t 2 =0
u ¢ ¢ +u- a u/t 2 =0
u ¢ ¢ +(1- a /t 2 )u=0, где a = m 2 -1/4.
Покажем, что нули вещественного решения v(t) уравнения (3.10) образуют при t>0 такую последовательность t 1 <t 2 <…, что t n -t n-1 ® p при n ® ¥ .
Так как в уравнении
u ¢ ¢ +(1- a /t 2 )u=0, т.е. уравнение
u ¢ ¢ +(1-( m 2 -1/4)/t 2 )u=0
m - постоянное число, то при m ³ 1/4 и при t – достаточно большое, то выражение
1-( m 2 -1/4)/t 2 ® 1, т.е. если уравнение
u ¢ ¢ +(1-( m 2 -1/4)/t 2 )u=0
сравнить с уравнением u ¢ ¢ +u=0, то расстояние между последовательными нулями стремится к p , т.е. t n -t n-1 ® p при n ® ¥ .
Теорема 3.2
(вторая теорема сравнения Штурма).
Пусть выполнены условия первой части теоремы
3.1
и функция
![]() имеет точно n нулей при
имеет точно n нулей при
![]() . Тогда соотношение
(3.4)
выполняется при
. Тогда соотношение
(3.4)
выполняется при
![]() [где выражение в правой (соответственно левой) части
(3.4)
при
[где выражение в правой (соответственно левой) части
(3.4)
при
![]() полагается равным
полагается равным
![]() ,
если
,
если
![]() (соответственно,
(соответственно,
![]() )].
Кроме того, при
)].
Кроме того, при
![]() в
(3.4)
имеет место строгое неравенство, если выполнены условия последней части теоремы
3.1.
в
(3.4)
имеет место строгое неравенство, если выполнены условия последней части теоремы
3.1.
Доказательство
этого утверждения содержится по существу в доказательстве теоремы 3.1, если заметить, что из предположения о числе нулей функции
![]() вытекает последнее неравенство в следующей цепочке:
вытекает последнее неравенство в следующей цепочке:
![]() . Аналогично, в предположениях последней части теоремы доказательство теоремы 3.1 дает неравенство
. Аналогично, в предположениях последней части теоремы доказательство теоремы 3.1 дает неравенство
![]() .
.
Использованная литература:
- Ф. Хартман. Обыкновенные дифференциальные уравнения: Учебн. пособие./ Пер. с англ. И.Х.Сабитова, Ю.В.Егорова; под ред. В.М.Алексеева.-М.: изд.”Мир”, 1970г.-720 с.
- В.В.Степанов. Курс дифференциальных уравнений. Гос.изд. “Технико-теор. литер.”-М., 1953г.-468 с.
- Большая Советская Энциклопедия. /Под ред. А.М.Прохорова. Изд. 3-е., М., “Советская Энциклопедия”, 1978г., т.29. “Чачан-Эне-ле-Бен.” – 640 с.
- Г.Вилейтнер. “История математики от Декарта до середины 19-го столетия.” М., изд. “Наука.”, 1966г. – 508 с.
- История математики с древнейших времён до начала 19-го столетия. /Под ред. Юшкевича А.П., т.3 /Математика 18-го столетия/., изд. “Наука.”, М., 1972г. – 496 с.
