Индексные числа
Индексные числа используются при описании экономических переменных. Они показывают, насколько изменилась какая либо величина за определенный промежуток времени. Например, когда говорят, что индекс прожиточного минимума составляет 120 по сравнению 1994 годом, то это означает что прожиточный минимум увеличился на 20 % за период, прошедший с 1994 года. Индексные числа также применяются для измерения динамики уровня производительности, безработицы и заработной платы.
Директор завода хотел бы сравнить затраты на производство единицы продукции с затратами которые были шесть месяцев назад.
Исследовательская группа медиков хотела бы сопоставить количество случаев заболевания гриппом в данном году с данными по предшествующему году; покупатель хочет узнать, каким ожидается рост цен на мясные продукты, чтобы соответствующим образом планировать свой бюджет и т. п. В каждом из перечисленных случаев необходимо определить степень изменения измеряемого показателя и выразить ее конкретным числом.
1. Определение простого индексного числа.
Индексное число вычисляется нахождением отношения между текущим и базовым значениями показателя. Затем, умножая полученный результат на 100, получаем процентное выражение индекса. Это окончательное значение называется относительным процентом. Заметим, что индексное число для базовой точки всегда составляет 100%.
Вычисление простого индекса. Статистическое управление располагает данными, характеризующими число вновь зарегистрированных структур бизнеса. Данные показывают, что в 1974 г. было создано 9300 новых структур, в 1984 г. - 9600 и в 1989 г. -10100. Приняв 1974 г. за базовый, можно подсчитать простой индекс, отражающий количественные изменения, как показано в табл. 1 . 1. Проведя эти вычисления, мы приходим к выводу, что количество новых фирм в 1979 г. имеет индекс 70 относительно 1974 г. Другими словами, число новых структур бизнеса в 1979 г. составило 70% от их числа в 1974 г.
Типы индексов.
Существует три основных типа индексов: ценовой, количественный и стоимостной .
Ценовой индекс используется наиболее часто. Он применяется для сравнения уровня цен одного периода с другим. Широко известный индекс потребительских цен, предоставляемый Статистическим управлением, показывает общее изменение цен на целый ряд потребительских товаров и услуг и используется как показатель уровня жизни
Таблица 1.1
Подсчет индексных чисел (базовый год -1974)
|
Год
(1) |
Количество новых структур*1000 (2): |
Отношение
|
Индекс или относ процент:(3)*100 (4). |
|
1974 1979 1984 1989 |
9.3 6.5 9.6 10.1 |
9.3:9.3 = 1.00 6.5:9.3=0.70 9.6:9.3 = 1.03 10.1 :9.3 = 1.09 |
0.70*100=70 1.03 * 100 = 103 I11.09 * 100 = 109 |
Количественный индекс показывает, как переменная, отражающая число или количество, изменяется во времени. В нашем примере был вычислен именно количественный индекс, определяющий соотношение между данными за 1979 г., 1984г., 1989 г. и данными за базовый 1974 г.
Часто индекс характеризует изменение переменной во времени, как и в случае временных рядов. В то же время, его можно использовать и для оценки изменения показателей в зависимости от места сбора информации. Это достигается одновременным сбором данных в различных местах с их последующим сравнением. Например, сравнительный индекс прожиточного минимума показывает, что, исходя из стоимости основных товаров и услуг, дешевле жить в Остине (штат Техас), чем в Нью-Йорке.
Стоимостной индекс характеризует изменения в общей стоимости денежных средств. Таким образом, он определяет изменения в стоимости доллара как переменной. При подсчете стоимостного индекса учитывают ценовые и количественные изменения для получения наиболее полной информации. В нашем примере- был определен лишь количественный индекс. Однако мы могли бы рассмотреть и долларовый эффект при помощи подсчета общей капитализированной стоимости для рассматриваемых лет. В (табл 1 . 2 ) представлены соответствующие стоимостные индексы для 1979, 1984 и 1989 гг. Согласно этим расчетам, стоимостной индекс предприятий в 1989 г. был равен 160.
Таблица 1.2
Подсчет стоимостного индекса (1974 г. - базовый)
|
Год
(1) |
Общая стоимость (млн. долл.) (2) |
Отношение (2): 18.4 (З) |
Индекс
|
|
1974 1979 1984 1989 |
18.4 14.6 26.2 29.4 |
18.4:18.4 = 1.00 14.6:18.4=0.79 26.2:18.4 = 1.42 29.4 :18.4 = 1.60 |
1.00* 100 = 100 0.79*100= 79 1.60* 100 = 142 1.60 * 100 = 160 |
Сводный индекс характеризует свойства группы изменяющихся переменных. Индекс потребительских цен определяет общий уровень цен на определенные товары и услуги, объединяя индивидуальные цены на товары и услуги в одном значении сводного ценового индекса.
Наиболее часто индексные числа применяются в качестве конкретного конечного результата. Такие показатели, как индекс потребительских цен. часто встречаются в прессе как общие оценки состояния экономики.
Менеджеры используют индексы как часть промежуточных расчетов. В табл. 1 . 3 показана еженедельная зарплата секретаря за несколько лет, соответствующий потребительский ценовой индекс и подсчет реальной зарплаты секретаря. Номинальная зарплата секретаря заметно увеличилась, но ее реальная покупательная способность росла не столь быстрыми темпами. Это можно объяснить одновременным ростом индекса прожиточного минимума со 100 до 200 единиц.
Таблица 1.3
Подсчет реальной заработной платы
|
Год
(1) |
Недельная зарплата (долл.) (2) |
Потребит. ценовой индекс (3) |
(4) |
Реальная зарплата, ( долл.) (5) |
|
1973 1979 1989 |
114.75 145.50 472.98 |
100 123 200 |
114.75 * 100:100 145.50 * 100:123 472.98*100:200 |
114.75 118.29 236.44 |
Проблемы, связанные с индексными числами.
Искажения, возникающие при использовании индексных чисел, могут быть вызваны следующими факторами:
1. Ограниченность данных. Иногда довольно трудно найти подходящие данные для вычисления индекса. Например, коммерческий директор небольшой авиастроительной компании хотел бы подсчитать индекс, характеризующий сезонные различия в объеме продаж небольших самолетов. Если он располагает данными только по годовому объему продаж, то определить сезонные колебания будет невозможно.
2. Несравнимость индексов. Часто пытаются сравнивать один индекс с другим после того, как в технологии производства или в общей экономической ситуации произошли радикальные изменения. Если сравнивать цены на автомобили в 1979 г. и в 1989 г., то выяснится, что цены в значительной степени выросли. Однако, это сравнение не учитывает технологического прогресса в автомобилестроении за эти 10 лет.
3. Неправильно выбранный вес так же могут привести к искажениям индекса. В процессе подсчета сводного индекса необходимо учитывать, что изменения одних переменных могут быть важнее, чем изменения других. Влияние на экономику 50-ти центового увеличения в цене за один галлон бензина не может быть компенсировано уменьшением цен на автомобили на те же 50 центов. Очевидно, что увеличение цены одного галлона на 50 центов имеет гораздо большее влияние на потребителя. Следовательно, большой вес должен быть присвоен возросшей цене на горючее, чем снижению цен на автомобили.
4. Искажение индекса может являться результатом неправильно выбранной базы. Иногда фирма выбирает такую базу, которая автоматически приводит к результату, отражающему интерес самой фирмы. Предположим, что общество по борьбе с чрезмерным расходом нефти хочет выставить нефтеперерабатывающие компании в плохом свете. Оно может измерять доходы текущего года, приняв в качестве базы какой-либо убыточный год. Тогда, несомненно, индекс отразит значительное увеличение доходов компании. С другой стороны, общество, выступающее за неограниченное потребление нефти, хотело бы показать, что в текущем году доходы от продажи нефти были минимальными. Тогда для базы можно выбрать год с весьма высокой прибылью. В результате, индекс покажет незначительное увеличение или даже сокращение доходов от продажи нефти. Следовательно, особое внимание должно уделяться тому, как и почему был выбран данный базовый период, и лишь затем делать выводы на основе сравнения индексных чисел.
2. Невзвешенный агрегативный (совокупный) индекс.
Самой простой формой сводного составного индекса является невзвешенный агрегативный индекс. Невзвешенный означает, что все значения, рассматриваемые в процессе подсчета индекса, входят с одинаковым весом. Агрегативный (совокупный) означает, что мы суммируем все значения. Главное преимущество этого индекса - его простота.
Подсчет невзвешенного совокупного индекса. Невзвешенный совокупный индекс вычисляется сложением всех элементов для данного временного периода с последующим делением результата на сумму этих же элементов для базового периода. Формула для подсчета невзвешенного совокупного индекса ( НСИ ):
НСИ=
![]() *100 (2.1)
где
*100 (2.1)
где
P 0 - количество каждого элемента для базового года;
P 1 - количество каждого элемента для текущего года.
Заметим, что в качестве P 0 и P 1 мы можем подставлять в эту формулу цены или стоимости для нахождения соответственно ценового или стоимостного индексов. Хотя индексы и выражены в виде процента, обычно используются только их значения и опускается знак процента при обработке индексных чисел.
Применение невзвешенного индекса.
В табл. 2.4 показано вычисление этого индекса. В данном примере мы определяем изменения в общем уровне цен на основе изменений цен на несколько наименований товаров. Цены 1984 г. являются базовыми значениями, которые сравниваются с ценами 1989г.
Таблица 2.4
Подсчет невзвешенного индекса
|
Элементы совокупного |
Цены ( долл.) |
|
|
индекса |
1984 г ( P 0) |
1989 г. (P 1) |
|
Молоко (1 галлон) Яйца (1 дюжина) Гамбургер (1 фунт) Бензин (1 галлон) |
1.92 0.81 1.49 1.00 |
3.40 1.00 2.00 1.17 |
|
S P 0 = 5.22 |
S P 1 =7.57 |
|
Невзвешенный совокупный индекс =
![]() *100=
*100=
![]() *100=145
*100=145
Интерпретация индекса.
Используя данный расчет, мы определяем, что ценовой индекс, описывающий изменения цен на эти товары с 1984 по 1989 гг., составляет 145. Таким образом, если элементы этой группы представляют общий уровень цен, то можно сказать, что цены выросли на 45 %. В то же время, от четырех наименований товаров нельзя ожидать точного отражения изменения цен на все товары и услуги.
Предположим, что мы добавили в табл. 2.4 изменения в цене на карманные калькуляторы. 1984г. вновь будет базовым, с которым сравниваются цены 1989г. (табл. 2.5 ). Интуитивно понятно, что предыдущий индекс, равный 145, есть более точная оценка общего поведения цен, чем 92 т.к. цены на большинство товаров выросли в период с 1984 по 1989 год. Таким образом, главный недостаток невзвешенного индекса заключается в следующем: он не придает большего значения (веса) наиболее часто используемым наименованиям продукции. (Семья в год может купить 50 дюжин яиц, но было бы странно, если бы она покупало такое же количество калькуляторов).
Включение в индекс товаров, цены на которые подвержены лишь незначительным колебаниям, может привести к серьезным искажениям, - по этой причине в важных исследованиях не принято использовать этот индекс. Его недостатки приводят нас к применению более сложных взвешенных индексов.
Таблица 2.5
Подсчет невзвешенного индекса
|
Элементы совокупного |
Цены ( долл.) |
|
|
индекса |
1984 г ( P 0) |
1989 г. (P 1) |
|
Молоко (1 галлон) Яйца (1 дюжина) Гамбургер (1 фунт) Бензин (1 галлон) Карманный калькулятор (1 шт.) |
1.92 0.81 1.49 1.00 15.00 |
3.40 1.00 2.00 1.17 11.00 |
|
S P 0 = 20.22 |
S P 1 =18.57 |
|
![]()
3 Взвешенный совокупный индекс (ВСИ).
Как уже было сказано выше, иногда при подсчете индекса изменениям в некоторых переменных необходимо приписывать большую важность (вес). Это так же позволяет улучшить точность оценки общего уровня цен. Проблема состоит в том, какой вес присвоить той или иной переменной в группе элементов индекса.
Общая формула для подсчета взвешенного совокупного ценового индекса ( ВСИ ):
ВСИ=
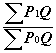 *100, (3.2)
где
*100, (3.2)
где
P 1 - стоимость каждого элемента в группе в текущем году;
P 0 - стоимость каждого элемента в группе в базовом году;
Q - выбранный количественный весовой фактор.
Рассмотрим пример в табл. 3.6 . Каждый из элементов группы взят из табл. 2.5 и взвешен в соответствии с объемом продаж. Данный расчет подтверждает наше интуитивное мнение, что общий уровень цен вырос (индекс равен 129).
Таблица З.6
Подсчет взвешенного совокупного индекса
|
Элементы |
Объем |
P 0 |
P 1 |
QP 1 |
Q |
|
совокупного |
млрд. |
Цены ( долл.) |
Взвешенные объемы продаж |
||
|
индекса |
(1) |
1984г. (2) |
1989г. (3 ) |
(2)*(1) |
(3)*(1) |
|
Молоко Яйца Гамбургер Бензин Калькулятор |
3.500 (дюж.) 11.000 (фунт.) 154.000 (галл.) 0.002 (шт.) |
1.92 0.81 1.49 1.00 15.00 |
3.40 1.00 2.00 1.17 11.00 |
38.40 2.84 16.39 154.00 0.03 |
68.00 3.50 22.00 180.18 0.02 |
|
S QP 0 = 211.66 |
S QP 1 =273.70 |
||||
ВСИ=
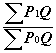 *100=
*100=
![]()
Обычно в качестве весового фактора при подсчете данного индекса используется количество потребления определенных наименований продукции. Это приводит нас к важному вопросу при применении данного процесса: какие именно количества необходимо использовать?
Три способа выбора весов.
Существует три способа выбора весов. Первый использует объем потребления продукции в течение базового периода при подсчете каждого индексного числа. Этот метод называется методом Ласпере (по имени автора метода). Второй использует количество потребляемой продукции в течение рассматриваемого периода (для каждого индексного числа). Это метод Пааше. Третий способ назван совокупным методом фиксированных весов. В этом случае выбирается один период и его количественные характеристики используются для нахождения всех индексов. (Заметим, что, если выбранный период - базовый, то данный метод сводится к методу Ласпере.
Метод Ласпере.
Метод Ласпере, в котором используется объем потребления продукции за базовый период, применяется наиболее широко, т.к. в нем используется количественные характеристики лишь для данного периода. Менеджеры так же могут непосредственно сравнивать индекс одного периода с другим, поскольку каждое индексное число зависит от одной и той же базовой цены и количества. Предположим, что ценовой индекс производства стали составлял 103 в 1986 г. и 125 в 1989 г. Используя базовые цены и объем потребления продукции в 1986 г., компания сделала вывод, что общий уровень цен вырос на 22% с 1986 по 1989 гг. Для подсчета индекса Ласпере сначала цена в текущем периоде умножается на количество в базовом периоде (для каждого элемента группы), затем результирующие значения суммируются. Та же процедура выполняется для базового периода (цена каждого элемента умножается на количество, затем производится суммирование полученных чисел). Поделив первую сумму на вторую и умножив результат на 100, получаем значение индекса Ласпере. Формула подсчета индекса Ласпере:
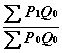
Q 0 - объем продаж в базовый период;
P 1 - цены в текущем году;
P 0 - цены в базовом году.
Пример: Предположим, что необходимо определить изменения в уровне цен между 1985 и 1989 гг. В табл. 3.7 приведено вычисление индекса Ласпере. Интерпретация вычисленного индекса: если мы имеем репрезентативную выборку товаров, то можно заключить, что общий ценовой индекс для 1989 г. составил 121 (при условии, что для 1985 г. - 100), или, что то же самое, цены выросли на 21%. Отметим, что мы использовали средний объем потребления товаров в 1985 г., а не совокупный объем потребления. В действительности это не играет большой роли, пока мы применяем одинаковые количественные характеристики в процессе вычисления индекса. Обычно выбирается наиболее простая количественная характеристика.
Таблица 3.7
Подсчет индекса Ласпере
|
Элементы совокупного индекса
(1) |
P 0 Базовая цена 1985 г (долл.)
(2) |
P 1 Текущая цена 1989 г. (долл.) (3 ) |
Q 0 Среднее количество продуктов, потребленных семьей в 1985 г. (4) |
P 0 Q 0 (4)*(2) (долл.)
(5) |
P 1 Q 0 (3)*(4) (долл.)
(6) |
|
Хлеб, бух. Картофель, фунт. Курица, шт. |
0.91 0.79 3.92 |
1.19 0.99 4.50 |
200 300 100 |
182 237 392 |
238 297 450 |
|
S |
811 |
985 |
.
Ценовой индекс Ласпере =
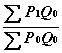 * 100 = 121
* 100 = 121
Преимущества метода Ласпере:
1) Возможность сравнивать один индекс с другим. Если бы в предыдущем примере у нас были бы цены 1986 г., то мы смогли бы найти значение общего ценового индекса для 1986 г. Этот индекс можно было бы непосредственно сравнивать с индексом для 1989 г. за счет использования одних и тех же базовых количеств.
2) Многие широко используемые количественные характеристики не вычисляются ежегодно. Фирму, например, может интересовал тот показатель, который подсчитывается один раз в 10 лет. И, поскольку метод Ласпере использует только одну переменную Q 0 (относящуюся к базовому году), то фирме нет необходимости искать ежегодные значения для подсчета количественной характеристики.
Главный недостаток метода Ласпере: Он не учитывает изменения в структуре потребления. Продукция, пользовавшаяся большим спросом всего несколько лет назад, может оказаться совершенно невостребованной сегодня. Если количественные характеристики базового года значительно отличаются от характеристик рассматриваемого периода, то изменение цены на эту продукцию плохо характеризует изменение общего уровня цен.
Метод Пааше
Нахождение индекса Пааше сходно с нахождением индекса Ласпере. Различие "Заключается в том, что в методе Пааше используется количественная мера для текущего периода, как в методе Ласпере. Последовательность вычислений:
1) Цена текущего периода умножается на количество каждого товара из группы в текущем периоде. Результаты складываются.
2) Цена базового периода умножается на количество каждого товара в текущем периоде. Результаты складываются.
- Первая сумма делится на вторую, а результат умножается на 100 для представления индекса в виде процента.
Индекс Пааше =
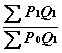 * 100, (3.4)
где
* 100, (3.4)
где
P 1 - цена текущего периода;
P 0 - цена базового периода;
Q 1 - Количественные характеристики текущего периода.
Используя эту формулу, мы можем пересмотреть расчеты в табл. 3.7 . Заменим количество потребленной продукции для 1985 г. на данные 1989 г. В табл. 3.8 представлены новые вычисления для этой задачи.
Таблица 3.8
Подсчет индекса Пааше
|
Элементы совокупного индекса
(1) |
P 0 Базовая цена 1985 г (долл.)
(2) |
P 1 Текущая цена 1989 г. (долл.) (3 ) |
Q 1 Среднее количество продуктов, потребленных семьей в 1989 г. (4) |
P 0 Q 1 (4)*(2) (долл.)
(5) |
P 1 Q 1 (3)*(4) (долл.)
(6) |
|
Хлеб, бух. Картофель, фунт. Курица, шт. |
0.91 0.79 3.92 |
1.19 0.99 4.50 |
200 100 300 |
238 99 1350 |
182 79 1176 |
|
S |
1687 |
1437 |
Ценовой индекс Пааше =
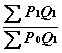 * 100 = 117
* 100 = 117
Интерпретация различий между двумя методами. В данном случае мы определили, что ценовой индекс для 1989 г. составил 117, а индекс Ласпере равнялся 121 (табл. 3.7 ). Разница в этих индексах отражает изменения в структуре потребления (для трех элементов данной группы).
Преимущества метода Пааше: Этот метод наиболее точен, так как в нем учитываются эффекты изменения в цене и структуре потребления. Следовательно, он лучше отображает изменения в экономике, чем индекс Ласпере. В нашем примере метод Пааше характеризует склонность к менее дорогим товарам и услугам, так как он показывает увеличение уровня цен на 17%, а не на 21% (согласно методу Ласпере).
Недостатки: Этот метод неудобен тем, что необходимо вычислять количественные характеристики для каждого рассматриваемого периода. Часто подобного рода информация недоступна, или ее получение сопряжено с большими затратами. Например, трудно найти надежный источник информации о годовом объеме потребления 100 пищевых продуктов в различных странах в течении нескольких лет. Значение ценового индекса Пааше есть результат как ценовых, так и количественных изменений относительно базового периода. Поскольку количественные характеристики, используемые для одного индексного периода, часто отличаются то характеристик другого индексного периода, то становится невозможным объяснить различия между индексами, вычисленными для этих периодов, только изменением уровня цен. Поэтому трудно сравнивать индексы Пааше, полученные для разных периодов времени.
Точный ценовой индекс (индекс Глушенкова).
Ранее говорилось, что при подсчете индекса некоторым переменным следует приписывать большую важность чем другим. В ценовых индексах весом мы выбирали потребленной продукции. Мы показываем каково значение данного товара на ценовой индекс в зависимости от количества его продаж и потребления, т.е. наиболее употребляемые товары и будут оказывать наибольшее воздействие на ценовой индекс. Но выбирая в качестве веса количество потребленной продукции в течении рассматриваемого или базового периода не учитывается, что вкусы людей меняются и соответственно значение переменных в различных периодах - различно. Чтобы избавиться от этого недостатка нужно присваивать переменным рассматриваемого и базового периода свои веса (в данном случае количество потребленной продукции). Формула вычисления индекса будет иметь следующий вид:
Индекс=
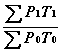 * 100, (3.5)
где
* 100, (3.5)
где
P 1 - цена текущего периода;
P 0 - цена базового периода;
T 0 - вес продукции в базовом периоде;
T 1 - вес продукции в текущем периоде.
Но следует учитывать объем потребленной продукции может меняться из-за роста населения. Рассмотрим табл. 3.9
Таблица 3.9
Подсчет ценового индекса
|
Элементы совокупного индекса
(1) |
P 0 Базовая цена 1985 г (долл.)
(2) |
P 1 Текущая цена 1989 г. (долл.)
(3 ) |
Q 0 Среднее количество продуктов, потребленных семьей в 1985 г. (4) |
Q 1 Среднее количество продуктов, потребленных семьей в 1985 г. (5) |
P 0 Q 0 (4)*(2) (долл.)
(6) |
P 1 Q 1 (3)*(5) (долл.)
(7) |
|
Хлеб, бух. Картофель, фунт. Курица, шт. |
0.91 0.79 3.92 |
0.91 0.79 3.92 |
200 300 100 |
300 450 150 |
182 237 392 |
273 356 588 |
|
S |
811 |
1217 |
Из таблицы видно, что спрос на данные товары из-за роста населения или каких то других причин вырос в 1.5 раза. Так как цены остались прежними, то ценовой индекс должен быть равен 100. Если считать по формуле (3.5) :
Индекс=
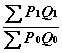 * 100=
* 100=
![]() *100=150
*100=150
Для избежания подобной ошибки следует брать в качестве веса не количество потребленной продукции, а отношение количества рассматриваемой потребленной продукции ко всему количеству потребленной продукции за указанный период:
Индекс=
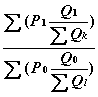 * 100, (3.6)
где
* 100, (3.6)
где
P 1 - цена текущего периода;
P 0 - цена базового периода;
Q 0 - количество потребленной продукции;
Q 1 - количество потребленной продукции в;
S Q l -
количество всей рассматриваемой продукции потребленной в базовом периоде;S Q k -
количество всей рассматриваемой продукции потребленной в текущем периоде.Рассмотрим тот же самый пример по формуле (3.6) с помощью таблиц 3.10 .
Таблица 3.10
Подсчет ценового индекса
|
Элементы совокупного индекса
(1) |
P 0 Базовая цена 1985 г (долл.) (2) |
P 1 Текущая цена 1989 г. (долл.) (3 ) |
Q 0 Среднее количество продуктов, потребленных семьей в 1985 г. (4) |
Q 1 Среднее количество продуктов, потребленных семьей в 1985 г. (5) |
Q 0 / S Q l (S (4))/(2) (долл.)
(6) |
Q 1 / S Q k (S (3))/(5) (долл.)
(7) |
|
Хлеб, бух. Картофель, фунт. Курица, шт. |
0.91 0.79
3.92 |
0.91 0.79
3.92 |
200 300
100 |
300 450
150 |
0.333 0.500
0.167 |
0.333 0.500
0.167 |
|
S |
600 |
900 |
Индекс=
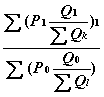 * 100=
* 100=
![]()
По сравнению с предыдущими методами данный метод обладает наибольшей точностью, но в данном случае необходимо знать цены и количество потребленной продукции как за базовый период, так и за рассматриваемый.
Совокупный метод взвешенных весов (СМВВ)
Совокупный метод взвешенных весов - третий способ приписывать веса элементам группы. Он схож и с первым, и со вторым методами. Однако в отличие от первых двух, он использует количественные характеристики репрезентативного периода. Репрезентативные веса называются фиксированными. Фиксированные веса и базовые цены не обязательно относятся к одному и тому же периоду времени.
Подсчет индекса
Данный индекс вычисляется следующим образом: цены текущего периода умножаются на фиксированные веса, и результаты суммируются. Затем цены базового периода умножаются на фиксированные веса, и результаты так же суммируются. Затем мы делим первую сумму на вторую и умножаем полученный результат на 100 для представления отношения в виде процента.
СМВВ=
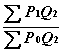 *100, (3.7)
где
*100, (3.7)
где
P 1 - цены текущего периода;
P 0 - цены базового периода;
Q 2 - Фиксированные веса.
Пример: Машиностроительной компании необходимо определить изменения в ценах на поставляемое сырье за период с 1969 по 1989 гг. Данные для вычисления индекса представлены в табл. 3.11. Исследование объемов закупок сырья в течении этого периода показало, что данные за 1982 г. наилучшим образом отражают структуру закупок сырья за все 20 лет. Уровень цен 1969 г. в данном примере является базовым. Расчеты показывают, что за 20 лет рост цен на сырье составил 157%.
Таблица З.11
Подсчет совокупного индекса взвешенных весов
|
Вид сырья |
Q 2 Объем. |
P 0 |
P 1 |
P 0 Q 2 |
P 1 Q 2 |
|
потребл в 1982г. (тыс.т) |
Средняя цена долл. за тонну |
(3)*(2) |
(4)*(2) |
||
|
(1) |
. (2) |
1984 г. (3) |
1989 г. (4) |
(5) |
(6) |
|
Уголь Железная руда Никель |
158 12 5 |
7.56 9.20 12.30 |
19.50 21.40 36.10 |
1194.48 110.40 61.50 |
3081.80 256.80 180.50 |
|
S Q 2 P i |
1366.38 |
3518.30 |
|||
Индекс =
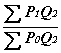 *100=257
*100=257
Преимущества совокупного метода фиксированных весов.
Основное преимущество данного ценового индекса заключается в гибкости при выборе базовой цены и фиксированных весов (количества). Во многих случаях тот период, который компания хотела бы использовать как базовый ценовой уровень, может иметь нетипичные для рассматриваемого периода характеристики уровня потребления. Следовательно, можно повысить точность данного индекса за счет выбора иного периода для нахождения фиксированных весов. Этот индекс так же позволяет изменить ценовую базу без изменения фиксированных весов, что очень выгодно, так как получить количественные характеристики для определенных периодов не всегда возможно.
- Методы относительных средних.
Метод невзвешенных относительных средних.
В качестве альтернативы рассмотренным методам построения индексов, мы можем использовать метод невзвешенных относительных средних. При подсчете простого индекса (табл. 1.1 ) уже была использована разновидность метода относительных средних. В том примере с одной измеряемой величиной мы подсчитали относительный процент путем деления количества корпораций в текущем году P 1 на их количество в базовом году P 2 затем умножили результат на 100 .
Подсчет невзвешенного индекса относительных средних: В случае более чем одного наименования продукта или рода деятельности, сначала находится отношение текущей цены к базовой (для каждого продукта) и каждое отношение умножают на 100 . Затем полученные значения складываются и результат делится на количество товаров.
![]()
Используя данные табл.3.4, рассчитаем индекс по методу невзвешенных относительных средних. Соответствующие вычисления приведены в табл. 4.12 : индекс общего уровня цен для 1989 г. составляет 138. В табл. 2.4 совокупный невзвешенный индекс был равен 145. Различие между двумя методами заключается в том, что в случае метода относительных средних мы рассчитываем среднее значение отношения цен по. всем продуктам, а в случае невзвешенного совокупного метода мы подсчитываем отношение сумм цен на все продукты. Заметим, что в рассматриваемом методе мы не присваиваем некоторым видам продуктов больший вес по сравнению с другими, а помещаем каждый элемент в относительную шкалу, где он представлен в виде процента, а не в виде денежной суммы. Таким образом каждый элемент группы оценивается относительно базы, принимаемой за 100%.
Таблица 4.12
Подсчет невзвешенного индекса относительных средних
|
Продукт (1) |
Цены 1984 г., долл. (2) |
Цены 1989 г., долл. (3) |
(3):(2) *100 (4) |
|
Молоко (1 галлон) Яйца (1 дюжина) Гамбургер (1 фунт) Бензин (1 галлон) |
1.92 0.81 1.49 1.00 |
3.40 1.00 2.00 1.17 |
177 123 134 117 |
|
S |
551 |
Невзв. индекс =
![]() =
=
![]() =138
=138
Метод взвешенных относительных средних.
Во многих задачах требуется определять индексные числа, исходя из взвешивания в соответствии с важностью (значимостью) того или иного элемента, поэтому более распространенным является метод взвешенных относительных средних. В разделе 3 , где подсчитывался взвешенный совокупный ценовой индекс, мы использовали объем потребления продукции в качестве весовых коэффициентов, тогда как в методе взвешенных относительных средних мы используем валовую стоимости каждого элемента группы (это величина получается умножением цены на количество).
Различные способы определения весов. В данном методе существует несколько способов определения взвешенных значений. Как и для индекса Ласпере, мы можем использовать базовую валовую стоимость, полученную умножением базового количества на базовую цену. Использование базовой стоимости приведет нас к тому же результату, что и в случае подсчета индекса по методу Ласпере. Поскольку результат одинаков, то решение об использовании метода Ласпере или метода взвешенных относительных средних часто зависит от возможности получения самих данных. Если более доступными являются данные о стоимости товаров, то используется метод взвешенных относительных средних. Мы применяем индекс Ласпере, если проще и дешевле получить количественные данные.
Подсчет взвешенного индекса относительного среднего:
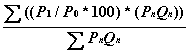
P n Q n - стоимость;
P 1 - цены текущего периода;
P 0 - цены базового периода.
P n и Q n - цены и количества, которые определяют значения, используемые нами как веса. В частности:
n = 0 для базового периода:
n = 1 для текущего периода;
n = 2 для фиксированного периода.
Следовательно, в случае базовых стоимостей формула (3.7) примет вид:
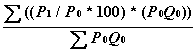
Соотношение между данными методом и методом Ласпере: расчет по формуле (4.10) эквивалентен расчету индекса Ласпере для любой задачи.
В особых случаях в общей формуле возможно использование стоимостей, полученных умножением цены из одного периода на количество из другого периода.
Пример: Данные, приведенные в табл. 4.13 были взяты из табл. 3.9 . Поскольку мы имеем цены и количества базового периода, то расчеты будем делать по формуле (4.10 ). Ценовой индекс, равный 122, немного отличается от 121, полученного в табл. 3.7 . Расхождение объясняется промежуточными округлениями.
Таблица 4.13
Подсчет взвешенного индекса относительных средних
|
Элементы |
P 0 |
P 1 |
Q 0 |
P 1 :P 0 |
P 0 Q 2 |
Взвеш. относит |
|
Совокупного |
Средняя цена (долл.) |
Среднее колич. |
(3):(2)* 100 |
Базовая стоимость |
процент |
|
|
Индекса (1) |
1985 г. (2) |
1989 г. (3) |
продуктов потреб. семьей в 1984 г. (4) |
(5) |
(2)*(4) (6) |
(5)*(6) (7) |
|
Хлеб, бух. Картофель,фунт Курица, шт. |
0.91 0.79 3.92 |
1.19 0.99 4.50 |
200 300 100 |
131 125 115 |
182 237 392 |
23842 29625 45080 |
|
S |
811 |
98547 |
||||
Индекс =
![]() = 122
= 122
Использование базовых, фиксированных и текущих стоимостей
В случаях базовых стоимостей P 0 Q 0 или фиксированных стоимостей P 1 Q 1 мы можем сравнивать уровни цен разных периодов. Однако при использовании текущих стоимостей P 1 Q 1 мы не можем непосредственно сравнивать значения разных периодов, так как и цены, и количества могли изменится. Поэтому при вычислении индекса взвешенных относительных средних обычно используются либо базовые, либо фиксированные стоимости.
5. Количественные и стоимостные индексы.
Использование количественного индекса.
До настоящего момента особое внимание уделялось ценовым индексам, но для описания количественных и стоимостных изменений так же можно использовать индексные числа. Наиболее часто применяются количественные индексы. Правление Федеральной Резервной Системы ежеквартально подсчитывает индексы и публикует их в статистическом ежемесячнике.
Индекс индустриального производства (ИИП) характеризует количество произведенной продукции в обрабатывающей промышленности, добывающих отраслях и в сфере коммунальных услуг. Этот количественный индекс рассчитывается по методу взвешенных относительных средних, в котором фиксированные веса (цены) и базовые количества продукции являются показателями 1977 года.
Преимущества количественного индекса.
В условиях инфляции количественный индекс обеспечивает более достоверную оценку реального производства сырья и готовой продукции, чем соответствующий стоимостной индекс. Для продукции сельского хозяйства использование количественного индекса является наилучшим, поскольку он устраняет эффект колебания цен. Количественный индекс часто используется для характеристики товаров, цены на которые подвержены значительным колебаниям. Любой из приведенных выше методов подсчета ценовых индексов может применятся и к количественным индексам. При вычислении ценовых индексов количества или стоимости берутся в качестве весовых коэффициентов.
Рассмотрим структуру количественного индекса, рассчитанного по методу взвешенных относительных средних. Процесс вычислений полностью совпадает с аналогичным ценовым индексом (формула 4.8 ). В этой формуле стоимость рассчитывается умножением количества на цену:
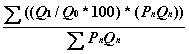 ,
(5.11)
где
,
(5.11)
где
Q 1 - количество для текущего периода;
Q 0 - количество для базового периода.
Обратимся к табл. 5.14 . Для вычислений используем формулу (4.9). Стоимость для базового периода определяется выражением P 0 Q 0 .
Таблица 5.14
Подсчет количественного индекса по методу взвешенных относительных средних
|
Элементы |
Q 0 |
Q 1 |
P 0 |
Q 1 :Q 0 |
P 0 Q 0 |
Взвеш. относит |
|
Совокупного |
Количество млрд. бушелей |
Цена за бушель |
(3):(2)* 100 |
Базовая стоимость |
процент |
|
|
Индекса (1) |
1985 г. (2) |
1989 г. (3) |
(долл.). 1984 г. (4) |
(5) |
(2)*(4) (6) |
(5)*(6) (7) |
|
Пшеница Кукуруза Соя |
29 3 12 |
24 2.5 14 |
3.80 2.91 6.50 |
83 83 117 |
110.21 8.73 78.0 |
9146.60 724.59 9126.00 |
|
S |
l96.93 |
18997.19 |
||||
Стоимостные индексы.
Недостаток стоимостного индекса заключается в том, что данный индекс характеризует общие изменения в совокупной стоимости некоторых переменных. Поскольку стоимость определяется как ценой, так и количеством, то стоимостной индекс фактически отражает совокупный эффект от изменения цен и количеств. Таким образом, с помощью стоимостного индекса невозможно оценить влияние каждой из этих составляющих на общее изменение стоимости.
Преимущество : Стоимостной индекс удобен для оценки общих изменений стоимости товаров и услуг
6. Заключение.
В этой работе были рассмотрены примеры с небольшими выборками и относительно короткими временными интервалами. В действительности индексные числа подсчитываются для групп с большим количеством элементов, при этом рассматриваются длительные периоды времени, что дает относительно точные оценки изменений. Однако, даже лучшие индексные числа несовершенны.
Проблемы построения.
Существует много проблем в построении индексных чисел, однако, среди них можно выделить три основные проблемы:
1. Выбор составляющих группы. Почти все индексы строятся с целью получения ответа на определенный вопрос. Следовательно, каждое включаемое в группу наименование зависит от этого вопроса.
Потребительский ценовой индекс показывает, каким образом цены на определенную группу товаров, покупаемых среднестатистическим американским гражданином, изменяется в течение определенного периода времени. Отсюда становится ясно, почему в эту выборку должны быть включены только те товары, которые отражают структуру потребления среднестатистической семьи. В то же время, данный индекс менее достоверно отражает изменения цен на товары, потребляемые семьями с низким или высоким доходом.
2. Выбор подходящих весов. В предыдущей части этой главы подчеркивалось, что веса должны представлять собой относительную значимость (важность) различных элементов. Однако, показатели, характерные для определенного периода времени, могут очень быстро устареть из-за резко меняющейся экономической ситуации или других факторов. Необходимо учитывать это при сравнении значений индексов, подсчитанных в разное время.
3. Выбор базового периода. Как правило, базовый период должен быть нормальным и недавним, что особенно желательно. "Нормальный" означает, что он не должен быть периодом резкого подъема (спада) или неустойчивости. Один из способов избежать использования неподходящего периода заключается в усреднении значений нескольких последовательных периодов, в результате мы получим нормальное значение. Статистическое управление США использует среднюю структуру потребления за 1982,1983 и 1984 годы для вычисления потребительского ценового индекса. Часто выбирают базовый период, который бы совпадал с базовым периодом одного или нескольких главных индексов, таких как индекс объема производства. Наличие общего базового периода позволяет соотносить вычисленные индексы с важными общенациональными показателями.
Проблемы, возникающие при интерпретации индекса.
В дополнение к трудностям при построении индексов существует несколько распространенных ошибок, совершаемых в процессе интерпретации индексов.
1. Выбор подходящих весов - весьма распространенная ошибка, допускаемая в процессе его анализа.
Потребительский ценовой индекс характеризует, каким образом изменились цены на определенную совокупность товаров, потребляемых средним американцем-горожанином. Несмотря на вполне конкретное определение, этому индексу часто приписывают способность отражать уровень жизни всех американцев. Хотя он в какой-то степени и имеет отношение к уровню жизни, но говорить, что он характеризует изменения в уровне жизни было бы неправильно.
2. Недостаток общего представления о публикуемых в печати индексах .
Типичная ошибка, связанная с этой проблемой, уже была рассмотрена выше. Ко всем широко известным индексам даются подробные пояснения, касающиеся их применения и истолкования.
3. Период времени и его влияние на индекс .
Факторы, используемые при расчете индекса, изменяются со временем. Такие изменения особенно свойственны весам, следовательно, сам индекс становится менее достоверным.
4. Качественные изменения.
Индексные числа часто критикуют за то, что они не отражают качественных изменений в анализируемых явлениях. Если качество действительно изменилось, то индекс занижает или преувеличивает изменения в уровне цен.
Например, если рассчитывается индекс с целью определить изменения в ценах на карманные калькуляторы за последние 10 лет, то результат будет занижать действительные изменения - ведь за этот период в донной отрасли было освоено много новых технологий, применение которых позволило значительно снизить цены.
