Задания 6, 7 для экзамена «Математика»
Вариант 1
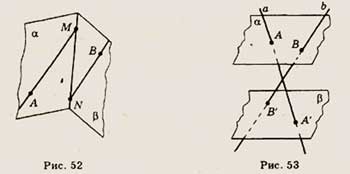
6. Туго натянутая нить последовательно закреплена в точках 1, 2, 3, 4 и 5, расположенных
на стержнях SA, SB и SC, которые не принадлежат одной плоскости (рис. 50). Скопируйте
рисунок, отметьте и обозначьте точки, в которых отрезки нити соприкасаются.
7. Отрезок AM перпендикулярен плоскости квадрата ABCD, ZABM = 30°. Найдите тангенс
угла АСМ.
Вариант 2
6. Туго натянутая нить последовательно закреплена в точках 1, 2, 3, 4, 5 и 6,
расположенных на стержнях SA, SB и SC, котоые не принадлежат одной плоскости
(рис. 51). Скопируйте рисунок, отметьте и обозначьте точки, в которых отрезки
нити соприкасаются.
7. Сторона квадрата равна 4 см. Точка, равноудаленная от всех вершин квадрата,
находится на расстоянии 6 см от точки пересечения его диагоналей. Найдите расстояния
от этой точки до вершин квадрата.
Вариант 3
6. В кубе ABCDA'B'C'D' из вершины D' проведены диагонали граней D'A, D'B' и
D'C. Сделайте рисунок. Как называется многогранник с вершинами D', А, В', С?
Имеет ли этот многогранник равные ребра? равные грани?
7. Треугольник ABC - - прямоугольный и равнобедренный с прямым углом С и гипотенузой
4 см. Отрезок СМ перпендикулярен плоскости треугольника и равен 2 см. Найдите
расстояние от точки М до прямой АВ.
Вариант 4
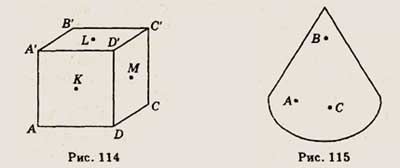
6. В кубе ABCDA'B'C'D' отмечены следующие точки: К-центр грани ВСС'В', L — центр
грани DCC'D' и М — центр грани ABCD. Сделайте рисунок. Как называется многогранник
CKLM? Имеет ли этот многогранник равные ребра? равные грани?
7. Радиус основания цилиндра равен 4 см, площадь боковой поверхности вдвое больше
площади основания. Найдите объем цилиндра.
Вариант 5
6. Точки пересечения высот всех граней правильной треугольной пирамиды являются
вершинами некоторого многогранника. Как называется этот многогранник? Имеет
ли он равные ребра? равные грани?
7. Отрезок АВ имеет с плоскостью а единственную общую точку А. Точка С делит
его в отношении 2 : 1, считая от точки Л. Через точки С и В проведены параллельные
прямые, пересекающие плоскость а соответственно в точках Cj и В1. Длина отрезка
АС1 равна 12 см. Найдите длину
отрезка АВ.
Вариант 6
6. Вершинами некоторого многогранника являются центр верхней грани куба и середины
всех сторон нижней его грани. Как называется этот многогранник? Сделайте рисунок
и обозначьте равные ребра многогранника; укажите, какие грани этого многогранника
равны между собой.
7. Треугольник ABC — прямоугольный и равнобедренный с прямым углом С и гипотенузой
6 см. Отрезок СМ перпендикулярен плоскости треугольника; расстояние от точки
М до прямой АВ равно 5 см. Найдите длину отрезка СМ.
Вариант 7
6. Плоскости а и Р, изображенные на.рисунке 52, пересекаются по прямой MN. Точка
А лежит в плоскости а, а точка В — в плоскости р. Определите, каково взаимное
расположение прямых AM и BN.
7. Основание прямой призмы — равнобочная трапеция, одно из оснований которой
в два раза больше другого. Непараллельные боковые грани призмы — квадраты. Высота
призмы равна б см. Площадь боковой поверхности призмы равна 144 см . Вычислите
объем призмы.
Вариант 8
6. На какие многогранники разбивает призму АВСА'В'С' плоскость, проходящая через
вершины А, В и С'? Сделайте рисунок.
7. Отрезок АВ имеет с плоскостью а единственную общую точку А. Через его середину
С и точку В проведены параллельные прямые, пересекающие плоскость а соответственно
в точках С1 и Вг Длина отрезка АС^ равна 8 см. Найдите дли- .
ну отрезка ABj.
Вариант 9
6. Изображенные на рисунке 53 прямые а и Ъ пересекают параллельные плоскости
аир соответственно в точках А, В н А', В'. Определите, каково взаимное расположение
прямых а и Ь.
7. Найдите объем тела, полученного при вращении прямоугольного треугольника
с катетом 3 см и прилежащим углом 30° вокруг меньшего катета.
Вариант 10
6. Сечение параллелепипеда ABCDA'B'C'D' проведено через точки А, В и середину
ребра СС". Каким многоугольником является это сечение? Сделайте рисунок
и отметьте равные стороны многоугольника.
7. В правильной четырехугольной пирамиде высота равна 12см, а высота боковой
грани — 15см. Найдите боковое ребро.
Вариант 11
6. Сечение параллелепипеда ABCDA'В'С'D' проведено через середины ребер АВ, AD
и А'В'. Каким многоугольником является это сечение? Сделайте рисунок и отметьте
равные стороны этого многоугольника.
7. Площадь осевого сечения цилиндра равна 20 см . Найдите площадь его боковой
поверхности.
Вариант 12
6. Куб ABCDA'B'C'D' рассечен на два многогранника плоскостью, проходящей через
середину ребра ЕЕ' перпендикулярно диагонали А'С. Каким многоугольником является
сечение? Какие особенности имеет этот многоугольник?
7. Середина С отрезка АВ принадлежит плоскости а. Через концы отрезка АВ проведены
параллельные прямые, пересекающие плоскость а в точках А1 и ЕГ Длина отрезка
А^С
равна 8 см. Найдите длину отрезка А^В^.
Вариант 13
6. Изображенные на рисунке 54 пр'ямые а и & пересекают параллельные плоскости
аир соответственно в точках А, В и А', В'. Скопируйте рисунок и определите,
каково взаимное расположение прямых а и 6.
7. Найдите объем тела, полученного при вращении прямоугольного треугольника
с катетом 6 см и гипотенузой 10 см вокруг большего катета.
Вариант 14
6. Куб рассечен плоскостью, проходящей через середины двух смежных сторон нижнего
основания и центр верхнего основания. Как называется многоугольник, полученный
в сечении? Сделайте рисунок и отметьте равные стороны этого многоугольника.
7. Треугольник ABC — прямоугольный и равнобедренный с прямым утлом С и гипотенузой
8 см. Отрезок СМ перпендикулярен плоскости треугольника и равен 3 см. Найдите
расстояние от точки М до прямой АВ.
Вариант 15
6. В кубе ABCDA'B'C'D' проведено сечение через середины ребер АА' и СС' и вершину
5. Каким многоугольником является это сечение? Сделайте рисунок и отметьте равные
стороны многоугольника.
7. Основание пирамиды — прямоугольный треугольник с катетами 6 см и 8 см. Высота
пирамиды проходит через середину гипотенузы треугольника и равна гипотенузе.
Найдите боковые ребра пирамиды.
Вариант 16
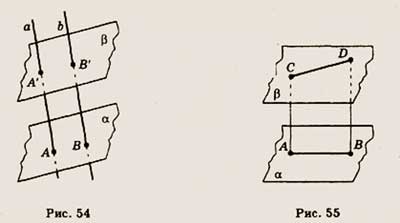
6. Изображенные на рисунке 55 плоскости а и Р параллельны. Отрезок АВ лежит
в плоскости а, а отрезок CD — в плоскости р. Определите, каково взаимное расположение
прямых АС и BD.
7. Если боковую поверхность конуса разрезать по образующей и развернуть на плоскости,
то получится круговой сектор с радиусом 4 см и центральным углом 120°. Найдите
объем этого конуса.
Вариант 17
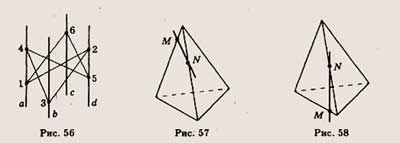
6. Туго натянутая нить последовательно закреплена в точках 1,2, 3, 4, 5 и 6,
расположенных на четырех попарно параллельных стержнях а, Ъ, с и d, никакие
три из которых не принадлежат одной и той же плоскости (рис. 56). Скопируйте
рисунок, отметьте и обозначьте точки, в которых отрезки нити соприкасаются.
7. Плоскость проходит на расстоянии 8 см от центра шара. Радиус сечения равен
15 см. Найдите площадь поверхности шара.
Вариант 18
6. Точки М и N расположены на ребрах треугольной пирамиды (рис. 57). Скопируйте
рисунок, отметьте и обозначьте точки, в которых прямая MN пересекает прямые,
содержащие другие ребра пирамиды.
7. Осевым сечением цилиндра является квадрат, диагональ которого равна 8 */2
см. Найдите объем цилиндра.
Вариант 19
6. Точки М к N расположены на ребрах треугольной пирамиды (рис. 58). Скопируйте
рисунок, отметьте точки, в которых прямая MN пересекает прямые, содержащие другие
ребра пирамиды.
7. Найдите площадь боковой поверхности тела, полученного при вращении прямоугольного
треугольника с катетом 3 см и противолежащим углом 30° вокруг большего катета.
Вариант 20
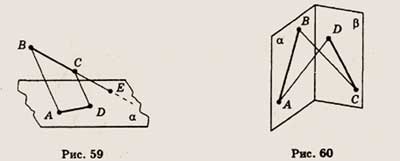
6. Продолжение отрезка ВС, изображенного на рисунке 59, пересекает плоскость
а в точке Е. Отрезок AD лежит в плоскости а. Скопируйте рисунок и изобразите
отрезки АС и BD. Определите, пересекаются ли эти отрезки.
7. Основание прямой призмы — прямоугольный треугольник с катетом 6 см и острым
углом 45°. Объем призмы
з равен 108 см . Найдите площадь полной поверхности
призмы.
Вариант 21
6. Отрезки АВ и CD, изображенные на рисунке 60, лежат в двух пересекающихся
плоскостях аир. Скопируйте рисунок и определите, каково взаимное расположение
прямых AD и ВС.
7. Основанием пирамиды является прямоугольный треугольник, гипотенуза которого
равна 15 см, а один из катетов — 9 см. Найдите площадь сечения, проведенного
через середину высоты пирамиды параллельно ее основанию.
Вариант 22
6. На какие многогранники разбивается параллелепипед ABCDA'B'C'D' плоскостью,
проходящей через вершины А, В' и D? Какие особенности имеют эти многогранники?
Сделайте рисунок.
7. Сторона квадрата равна 4 см. Точка, не принадлежащая плоскости квадрата,
удалена от каждой из его вершин на расстояние 6 см. Найдите расстояние от этой
точки до плоскости квадрата.
Вариант 23
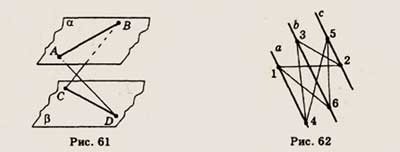
6. Изображенные на рисунке 61 плоскости а и (3 параллельны. Отрезок АВ лежит
в плоскости а, а отрезок CD в плоскости р. Определите, каково взаимное расположение
прямых AD иВС.
7. Основание пирамиды — прямоугольник со сторонами 6 см и 8см. Все боковые ребра
равны 13см. Найдите объем пирамиды.
Вариант 24
6. Туго натянутая нить последовательно закреплена в точках 1, 2, 3, 4, 5 и 6,
расположенных на параллельных стержнях a, b и с, не принадлежащих одной и той
же плоскости (рис. 62). Скопируйте рисунок, отметьте и обозначьте точки, в которых
отрезки нити соприкасаются.
*
7. Основание пирамиды — ромб с диагоналями 6 см и 8 см. Высота пирамиды опущена
в точку пересечения его диагоналей. Меньшие боковые ребра пирамиды равны 5 см.
Найдите объем пирамиды.
Вариант 25
6. В кубе проведено сечение через середины двух смежных сторон верхнего основания
и центр нижнего. Каким многоугольником является это сечение? Сделайте рисунок
и отметьте равные стороны этого многоугольника.
7. Объем шара равен Збя см . Найдите площадь поверхности
шара.
Вариант 26
6. Сечение правильной треугольной призмы проходит через центры оснований и одну
из вершин. Каким многоугольником является это сечение? Сделайте рисунок и отметьте
равные стороны этого многоугольника.
7. Три смежных ребра треугольной пирамиды попарно перпендикулярны и равны 6
см, 6 см и 8 см. Найдите площадь полной поверхности пирамиды.
Вариант 27
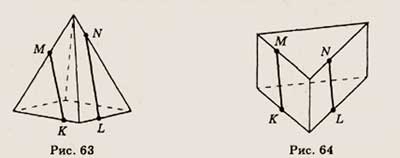
6. Точки К, L, М и N лежат на ребрах изображенной на рисунке 63 пирамиды. Скопируйте
рисунок и определите, имеют ли отрезки KN и LM общую точку.
7. Сумма площадей поверхностей двух шаров радиуса 4 см равна площади поверхности
некоторого большего шара. Каков объем этого большего шара?
Вариант 28
6. Точки К, L, М к N лежат на ребрах изображенной на рисунке 64 прямой призмы.
Скопируйте рисунок и определите, каково взаимное расположение прямых КМ и LN.
7. Найдите площадь полной поверхности тела, полученного при вращении прямоугольника
со сторонами 6 см и 10 см вокруг его оси симметрии, параллельной большей стороне.
Вариант 29
6. Точки М и N расположены на ребрах четырехугольной пирамиды (рис. 65). Скопируйте
рисунок, отметьте и обозначьте точки, в которых прямая MN пересекает прямые,
содержащие другие ребра пирамиды.
7. Образующая конуса равна 12 см и составляет с плоскостью основания угол 30°.
Найдите объем конуса.
Вариант 30
6. Точки М п N расположены на ребрах четырехугольной пирамиды (рис. 66). Скопируйте
рисунок, отметьте и обозначьте точки, в которых прямая MN пересекает прямые,
содержащие другие ребра пирамиды.
7. Найдите площадь полной поверхности тела, полученного при вращении равнобедренного
прямоугольного треугольника с катетом 8 см вокруг его оси симметрии.
Вариант 31
6. Вершинами многогранника являются середины сторон основания и середина высоты
правильной четырехугольной пирамиды. Как называется этот многогранник? Сделайте
рисунок и отметьте равные ребра этого многогранника.
7. Площадь боковой поверхности конуса равна 20тг см , а площадь его основания
на 4л см меньше. Найдите объем конуса.

Вариант 32
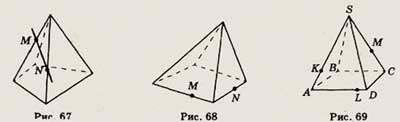
6. Точки М и N расположены на ребрах четырехугольной пирамиды (рис. 67). Скопируйте
рисунок, отметьте и постройте точку, в которой прямая MN пересекает плоскость
основания пирамиды.
g
7. Объем конуса с радиусом основания 6см равен 96л см . Найдите площадь боковой
поверхности конуса.
Вариант 33
6. Точки М и N расположены на ребрах четырехугольной пирамиды (рис. 68). Скопируйте
рисунок, отметьте и постройте точки, в которой прямая MN пересекает прямые,
содержащие ребра пирамиды.
7. Отрезок АВ пересекает плоскость а в точке С, которая делит
его в отношении 3:1, считая от точки А. Через концы отрезка АВ проведены параллельные
прямые, пересекающие плоскость а в точках А^ и В^. Длина отрезка А^С равна
15 см. Найдите длину отрезка А^В^.
Вариант 34
6. Точки К, L и М принадлежат ребрам изображенной на рисунке 69 пирамиды SABCD.
Скопируйте рисунок и отметьте точку N на ребре CD так, чтобы отрезки KN и LM
имели общую точку.
7. Высота конуса равна 12 см, а угол при вершине осевого сечения равен 120°.
Найдите площадь полной поверхности конуса.
Вариант 35
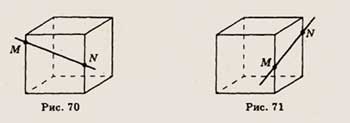
6. Точки М и N расположены на ребрах куба (рис. 70). Скопируйте рисунок, отметьте
и обозначьте точки, в которых прямая МЛ'" пересекает прямые, содержащие
другие ребра куба.
7. Прямоугольный треугольник с катетами 3 см и 4 см в первый раз вращается вокруг
большего катета, а во второй — вокруг меньшего. Сравните площади боковых поверхностей
получающихся при этом конусов.
Вариант 36
6. Точки М к N расположены на ребрах куба (рис. 71). Скопируйте рисунок, отметьте
и обозначьте точки, в которых прямая MN пересекает прямые, содержащие другие
ребра куба.
7. В правильной четырехугольной пирамиде сторона основания равна 10 см, а боковое
ребро — 13 см. Найдите высоту пирамиды.
Вариант 37
6. Куб ABCDA'B'C'D' рассечен на два многогранника плоскостью, проходящей через
середину ребра ВВ' перпендикулярно диагонали BD''. Каким многоугольником является
сечение? Сделайте рисунок и отметьте равные стороны этого многоугольника.
7. Радиус основания цилиндра равен 8 см, площадь боковой поверхности вдвое меньше
площади основания. Найдите объем цилиндра.
Вариант 38
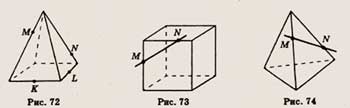
6. Точки К, L, М и N принадлежат ребрам изображенной на рисунке 72 пирамиды,
причем К и L — середины ребер. Скопируйте рисунок и определите, пересекаются
ли прямые KL и MN, отрезки KN и LM.
7. Площадь осевого сечения цилиндра равна 108 см , а его образующая в три раза
меньше диаметра основания. Найдите площадь полной поверхности цилиндра.
Вариант 39
6. Точки М я N расположены на ребрах куба (рис. 73). Скопируйте рисунок, отметьте
и обозначьте точки, в которых прямая MN пересекает прямые, содержащие другие
ребра куба.
7. Найдите площадь полной поверхности тела, полученного при вращении прямоугольного
треугольника с катетами 3 см и 4 см вокруг большего катета.
Вариант 40
6. Точки М и N расположены на ребрах треугольной пирамиды (рис. 74). Скопируйте
рисунок, отметьте и обозначьте точки, в которых прямая MN пересекает прямые,
содержащие другие ребра пирамиды.
7. Радиус основания цилиндра равен 6 см, высота в два раза меньше длины окружности
основания. Найдите площадь полной поверхности цилиндра.
Вариант 41
6. Точки К и L — вершины куба, изображенного на рисунке 75, точки М и N .— середины
его ребер. Определите, пересекаются ли отрезки KN и LM.
7. Найдите объем тела, полученного вращением прямоугольника со сторонами 4 см
и 6 см вокруг прямой; проходящей через середины его больших сторон.
Вариант 42
6. Точки К, L, М и N принадлежат ребрам изображенной на рисунке 76 пирамиды.
Скопируйте рисунок и определите, пересекаются ли прямые KL и MN, отрезки KN
и LM.
7. Сторона квадрата ABCD равна 2 см. Отрезок AM перпендикулярен плоскости квадрата,
ZABM = 60°. Найдите расстояние от точки М до прямой BD.
Вариант 43
6. Точки пересечения диагоналей всех граней правильной четырехугольной призмы
являются вершинами некоторого многогранника. Сделайте рисунок и отметьте равные
ребра этого многогранника.
7. Отрезок АВ имеет с плоскостью а единственную общую точку А. Точка С делит
отрезок AS в отношении 3 : 2, считая от точки А. Через точки С и Б проведены
параллельные прямые, пересекающие плоскость а соответственно в точках С, и В..
Длина отрезка АВ1 равна 15 см. Найдите длину отрезка АСГ

Вариант 44
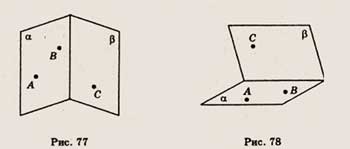
6. На рисунке 77 изображены пересекающиеся плоскости а и р. Точки А и Б принадлежат
плоскости а, а точка С лежит в плоскости р. Скопируйте рисунок и изобразите
на нем точку D, принадлежащую плоскости р, так, чтобы прямые АС и BD оказались
параллельными.
7. Треугольник ABC — прямоугольный и равнобедренный с прямым углом С и гипотенузой
6 см. Отрезок AM перпендикулярен плоскости треугольника, Z МСА = 60°. Найдите
длину отрезка МБ.
Вариант 45
6. На рисунке 78 изображены пересекающиеся плоскости а и р. Точки А и В принадлежат
плоскости а, а точка С лежит в плоскости р. Скопируйте рисунок и изобразите
на нем точку D, принадлежащую плоскости р, так, чтобы прямые АС и BD оказались
параллельными.
7. Через концы отрезка AJB, не пересекающего плоскость а, проведены параллельные
прямые, пересекающие плоскость а в точках А1 и Бр АА^ = 5 см, В^В = 8 см. Найдите
длину
отрезка, соединяющего середины отрезков АВ иА1В1.
Вариант 46
6. На рисунке 79 изображены пересекающиеся плоскости а и р. Точки А и В принадлежат
плоскости а, а точка С лежит в плоскости р. Скопируйте рисунок и изобразите
на нем точку D, принадлежащую плоскости р, так, чтобы отрезки AD и ВС оказались
пересекающимися.
7. Из точки О пересечения диагоналей квадрата ABCD к его плоскости восставлен
перпендикуляр ОМ так, что Z ОВМ = 60°. Найдите косинус угла АВМ.
Вариант 47
6. На рисунке 80 изображены пересекающиеся плоскости а и Р. Точки А и В принадлежат
плоскости а, а точка С лежит в плоскости р. Скопируйте рисунок и изобразите
на нем точку D, принадлежащую плоскости р, так, чтобы отрезки АС и BD оказались
пересекающимися.
7. Диагональ квадрата равна 6 см. Точка, равноудаленная от всех сторон квадрата,
находится на расстоянии 5 см от точки пересечения его диагоналей. Найдите расстояние
от этой точки до стороны квадрата.
Вариант 48
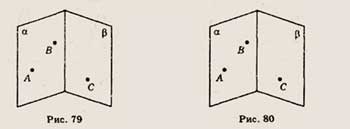
6. Туго натянутая нить последовательно закреплена в точках 1, 2, 3, 4 и 5, расположенных
на параллельных стержнях а, Ъ и с, не принадлежащих одной и той же плоскости
(рис. 81). Скопируйте рисунок, отметьте и обозначьте точки, в которых нити соприкасаются.
7. Найдите объем тела, полученного при вращении прямоугольника со сторонами
6 см и 10 см вокруг большей стороны.
Вариант 49
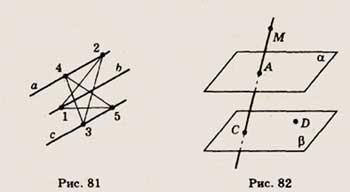
6. На рисунке 82 изображены параллельные плоскости аир. Точка А принадлежит
плоскости а, точки С и D лежат в плоскости р, а точка М принадлежит прямой АС.
Скопируйте рисунок и изобразите на нем точку В, принадлежащую плоскости а, так,
чтобы прямые-АС и BD пересекались в точке М.
7. Основание пирамиды — прямоугольный треугольник с катетами 6 см и 8 см. Высота
пирамиды, равная 12 см, делит гипотенузу этого треугольника пополам. Найдите
боковые ребра пирамиды.
Вариант 50
6. На рисунке 83 изображены параллельные плоскости а и Р. Точки А к В принадлежат
плоскости а, а точка С лежит в плоскости р. Скопируйте рисунок и изобразите
на нем точку .D, принадлежащую плоскости р, так, чтобы прямые АС и BD оказались
параллельными.
7. Через концы отрезка AS, имеющего с плоскостью а общую точку, проведены параллельные
прямые, пересекающие плоскость а в точках Ах и В^\ АА1 — 5 см. Длина отрезка,
соединяющего середины отрезков АВ и А1Б1, равна 8 см. Найдите длину отрезка
В^.
Вариант 51
6. На рисунке 84 изображены параллельные плоскости аир. Точки А и Б принадлежат
плоскости а, точка С лежит в плоскости р, а точка М принадлежит прямой ВС. Скопируйте
рисунок и изобразите на нем точку D, принадлежащую плоскости р, так, чтобы прямые
AD и ВС пересекались в точке М.
7. Найдите объем тела, полученного при вращении прямоугольного треугольника
с гипотенузой 10 см и острым утлом 30° вокруг меньшего катета.
Вариант 52
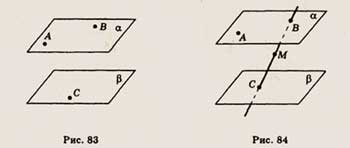
6. Точки Аи В лежат соответственно на нижнем и верхнем основаниях цилиндра,
изображенного на рисунке (рис. 85). Скопируйте рисунок и проведите отрезок АВ.
Определите, все ли точки отрезка АВ лежат на поверхности цилиндра.
7. В правильной треугольной пирамиде боковое ребро равно 10 см, а сторона основания
12 см. Найдите площадь полной поверхности пирамиды.
Вариант 53
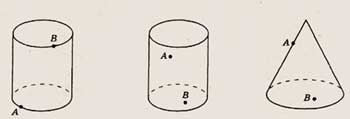
6. Точки А и В расположены на видимой части боковой поверхности цилиндра (рис.
86). Скопируйте рисунок и проведите отрезок АВ. Все ли точки отрезка АВ принадлежат
боковой поверхности цилиндра?
7. Основание пирамиды — ромб с диагоналями 30 см и 40 см. Вершины пирамиды удалены
от сторон основания на 13 см. Найдите высоту пирамиды.
Вариант 54
6. Точки А и В принадлежат боковой поверхности конуса (рис. 87). Скопируйте
рисунок и проведите отрезок АВ. Определите, все ли точки отрезка АВ лежат на
поверхности конуса.
7. В прямоугольнике ABCD АВ = 2 см, AD = 5 см. Отрезок AM перпендикулярен плоскости
прямоугольника, Z АВМ = 30°. Найдите объем многогранника MAB.D.
Вариант 55
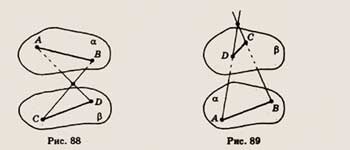
6. На рисунке 88 изображены отрезки АВ и CD, лежащие соответственно в плоскостях
а и р. Прямые AD и ВС пересекаются. Определите, каково взаимное расположение
плоскостей аир.
2
7. Площадь полной поверхности куба равна 24 см . Найдите его диагональ.
Вариант 56
6. На рисунке 89 изображены отрезки AS и CD, лежащие соответственно в плоскостях
аир. Прямые AD и ВС пересекаются. Определите, каково взаимное расположение плоскостей
а и р.
7. Площадь полной поверхности прямоугольного параллелепипеда равна 136 см ,
стороны основания 4 см и 6см. Вычислите объем прямоугольного параллелепипеда.
Вариант 57
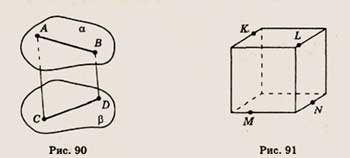
6. На рисунке 90 изображены отрезки AS и CD, лежащие соответственно в плоскостях
аир. Прямые АС и BD параллельны. Скопируйте рисунок и определите, каково взаимное
расположение плоскостей аи р.
7. Стороны основания прямоугольного параллелепипеда равны 3 см и 5 см, большая
из диагоналей его боковых граней образует с плоскостью основания угол 60°. Найдите
площадь полной поверхности параллелепипеда.
Вариант 58
6. Точки К, L, М и N принадлежат соответствующим ребрам куба, изображенного
на рисунке 91. Определите, пересекаются ли прямые KL и МN, отрезки KN и LM.
7. Осевым сечением цилиндра является квадрат, диагональ
которого равна 6 л/2 см. Найдите площадь полной поверхности цилиндра.
» Вариант 59
6. Сечение правильной треугольной призмы АВСА'В'С' проходит через ребро АБ и
точку пересечения медиан основания А'В'С'. Каким многоугольником является это
сечение? Сделайте рисунок и отметьте равные стороны этого многоугольника.
7. Отрезок, соединяющий конец диаметра нижнего основания цилиндра с центром
его верхнего основания, равен 2 см и наклонен к плоскости основания под углом
30°. Найдите площадь полной поверхности цилиндра.
Вариант 60
6. В правильной четырехугольной пирамиде проведено сечение через середины двух
смежных сторон основания и середину несмежного с ними бокового ребра. Каким
многоугольником является это сечение? Сделайте рисунок и отметьте равные стороны
многоугольника.
7. Радиус основания конуса равен 5 см, а образующая конуса равна 13 см. Найдите
объем конуса.
Вариант 61
6. Точки К и L — вершины куба, изображенного на рисунке 92, точки М и N — середины
его ребер. Определите, пересекаются ли прямые KL и MN, отрезки KN и LM.
7. Отрезок АВ пересекает плоскость а в точке С, которая делит его в отношении
3:5, считая от точки А. Через концы отрезка АВ проведены параллельные прямые,
пересекающие плоскость а в точках А1 и Вг Длина отрезка АХС равна
12 см. Найдите длину отрезка А1ВГ
Вариант 62
6. Точки К, L, М к N принадлежат ребрам изображенной на рисунке 93 пирамиды.
Скопируйте рисунок и определите, пересекаются ли отрезки KN и LM*.
7. Образующая конуса равна 5 см, площадь его боковой поверхности равна 15я см
. Найдите объем конуса.
Вариант 63
6. В KyQeABCDA'B'C'D' проведено сечение через середины ребер АВ, AD и ВВ'. Каким
многоугольником является сечение? Сделайте рисунок и отметьте равные стороны
этого многоугольника.
7. Высота цилиндра равна 6 см, а площадь его боковой поверхности вдвое меньше
площади его полной поверхности. Найдите объем цилиндра.
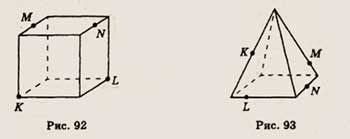
Вариант 64
6. Через середины двух сторон АВ и АС основания правильной треугольной пирамиды
SABC и точку пересечения медиан грани SBC проведено сечение. Каким многоугольником
является это сечение? Сделайте рисунок и отметьте равные стороны этого многоугольника.
7. Сторона квадрата ABCD равна 1 см. Отрезок AM перпендикулярен плоскости квадрата,
ZABM = 30°. Найдите расстоя.-ние от точки М до прямой BD.
Вариант 65
6. Точки К, L, М и N принадлежат ребрам изображенной на рисунке 94 пирамиды.
Определите, пересекаются ли прямые KL и MN, отрезки KN и LM.
7. Найдите площадь сечения шара радиуса 41 см плоскостью, проведенной на расстоянии
29 см от центра шара.
Вариант 66
6. Точка М — середина ребра AD куба, изображенного на рисунке 95. Скопируйте
рисунок и изобразите точку N, принадлежащую ребру CD, так, чтобы отрезки A'N
и С'М имели общую точку.
7. Квадрат со стороной 3 см вращается вокруг своей диагонали. Найдите площадь
поверхности тела вращения.
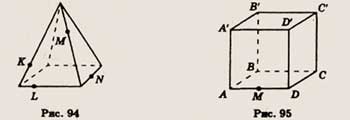
Вариант 67
6. Вершинами многогранника являются середины боковых ребер и центр основания
правильной пирамиды. Как называется этот многогранник? Сделайте рисунок и отметьте
равные ребра этого многогранника.
7. Круговой сектор с радиусом 10 см свернут в виде боковой поверхности конуса.
Высота конуса равна 8 см. Найдите центральный угол кругового сектора.
Вариант 68
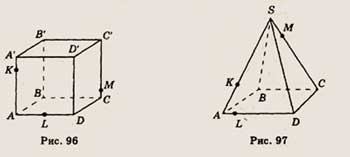
6. Точки К, L и М расположены на ребрах куба ABCDA'B'C'D', изображенного на
рисунке 96. Скопируйте рисунок и изобразите точку N, принадлежащую ребру CD,
так, чтобы отрезки KN и LM имели общую точку.
7. Квадрат со стороной 3 см вращается вокруг своей диагонали. Найдите объем
тела вращения.
Вариант 69
6. Точки К, L и М принадлежат ребрам изображенной на рисунке 97 пирамиды SABCD.
Скопируйте рисунок и отметьте точку N на ребре CD так, чтобы отрезки KN и LM
имели общую точку.
7. Найдите объем тела, полученного при вращении прямоугольника со сторонами
6 см и 8 см вокруг прямой, которая проходит через середины его меньших сторон.
Вариант 70
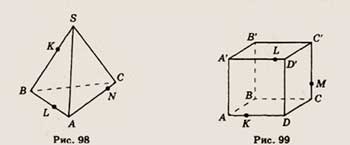
6. Точки К, L и N принадлежат ребрам изображенной на рисунке 98 пирамиды SASC.
Скопируйте рисунок и отметьте точку М на ребре SC так, чтобы отрезки KN и LM
имели общую точку.
7. Найдите объем тела, которое получено при вращении*квад-рата со стороной 7
см вокруг прямой, соединяющей середины противоположных сторон.
Вариант 71
6. Точки К, L и М лежат на ребрах куба ABCDA'B'C'D', изображенного на рисунке
99. Скопируйте рисунок и отметьте точку N на ребре C'D' так, чтобы отрезки KN
и LM пересеклись.
7. Высота конуса равна 8 см, объем 24я см . Найдите площадь полной поверхности
конуса.
Вариант 72
6. Вершины некоторого многогранника являются центрами пяти граней куба. Как
называется этот многогранник? Сделайте рисунок и отметьте равные ребра этого
многогранника.
7. Три одинаковых металлических куба с ребрами по 4 см сплавлены в один куб.
Определите площадь поверхности этого куба.
Вариант 73
6. Точки К, L и М принадлежат ребрам изображенной на ри- I сунке 100 пирамиды
SABCD. Скопируйте рисунок и отметь- I те точку N на ребре SC так, чтобы отрезки
KN и LM пересеклись.
7. Образующая конуса составляет с плоскостью его основания угол в 30°, а радиус
основания конуса равен 6 см. Найдите площадь полной поверхности конуса.
Вариант 74
6. Точки К, L, М и N лежат на ребрах куба (рис. 101). Скопируйте рисунок и определите,
существует ли точка пересечения отрезков KN и ML.
7. Прямоугольный треугольник, гипотенуза которого равна 17 см, а один из катетов
равен 8 см, вращается вокруг своего большего катета. Найдите площадь поверхности
тела вращения.
Вариант 75
6. В правильной четырехугольной пирамиде проведено сечение через диагональ основания
параллельно непересекающемуся с ней боковому ребру. Каким многоугольником является
это сечение? Сделайте рисунок и отметьте равные стороны этого многоугольника.
7. Высота конуса равна 12 см, а его образующая равна 13 см. Найдите площадь
полной поверхности конуса.
Вариант 76
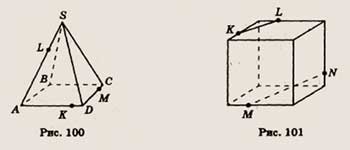
6. Точки К и N лежат на ребрах изображенной на рисунке 102 пирамиды, а точки
L и М принадлежат соответственно ее граням CSD и A5D. Скопируйте рисунок, изобразите
отрезки KL и MN и определите, имеют ли они общую точку.
7. Два металлических куба с ребрами 1 см и 2 см соответственно сплавлены в один
куб. Определите ребро этого куба.
Вариант 77
6. Точки К, L, М и N лежат на ребрах изображенной на рисунке 103 пирамиды. Скопируйте
рисунок и определите, каково взаимное расположение прямых KL и MN.
7. Два металлических куба с ребрами 1 см и 2 см сплавлены в один куб. Определите
полную поверхность этого куба.
Вариант 78
6. Правильная треугольная пирамида рассечена на два многогранника плоскостью,
проходящей через сторону основания и середину высоты пирамиды. Каким многоугольником
является это сечение? Сделайте рисунок и отметьте равные стороны этого многоугольника.
7. Высота конуса равна Ь см, а угол при вершине осевого сечения равен 120°.
Найдите объем конуса.
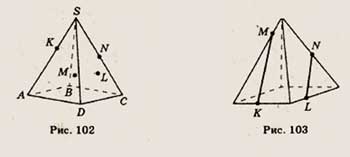
Вариант 79
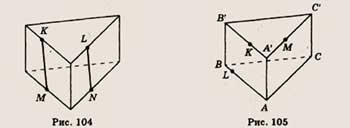
6. Точки К, L, М и N лежат на ребрах изображенной на рисунке 104 призмы. Скопируйте
рисунок и определите, имеют ли отрезки KN и ML общую точку.
7. К плоскости равнобедренного треугольника ABC с основанием ВС = 6 см и углом
120° при вершине проведен перпендикуляр AM. Расстояние от точки М до ВС равно
12 см. Найдите косинус линейного угла двугранного угла, образованного плоскостями
треугольников ABC и МВС. ,
Вариант 80
6. Точки К, L и М лежат на ребрах изображенной на рисунке 105 призмы. Скопируйте
рисунок и отметьте на ребре АС точку N так, чтобы отрезки KN и LM имели общую
точку.
7. Найдите объем тела, получение^ при вращении равнобедренного прямоугольного
треугольника с катетом 6 см вокруг его оси симметрии.
Вариант 81
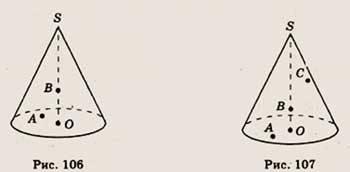
6. Точка А принадлежит основанию конуса, изображенного на рисунке 106, а точка
В — оси SO этого конуса. Скопируйте рисунок и отметьте точку С, в которой прямая
АВ пересекает боковую поверхность конуса.
7. Объем прямоугольного параллелепипеда равен 24 см , площадь основания 12 см
. Одна сторона основания в три раза больше другой. Вычислите площадь полной
поверхности параллелепипеда.
Вариант 82
6. Правильная четырехугольная пирамида рассечена на два многогранника плоскостью,
проходящей через сторону основания и медиану боковой грани. Каким многоугольником
является это сечение? Сделайте рисунок и отметьте равные стороны этого многоугольника.
7. Площадь осевого сечения цилиндра равна 64 см , а его образующая равна диаметру
основания. Найдите объем цилиндра.
Вариант 83
6. Точка А принадлежит основанию конуса, изображенного на рисунке 107, а точка
В — оси SO этого конуса. Скопируйте рисунок и определите, где, внутри или снаружи
конуса, расположена точка С прямой АВ.
7. Площадь полной поверхности прямоугольного параллелепипеда равна 136см , стороны
основания 4см и 6см. Вычислите диагональ прямоугольного параллелепипеда.
Вариант 84
6. На какие многогранники разбивает прямую призму АВСА'В'С' плоскость, проходящая
через вершины А, В и С'? Сделайте рисунок.
7. Шар с центром в точке О касается плоскости в точке А. Точка В лежит в плоскости
касания. Найдите объем шара, если АВ = 21 см, ВО = 29 см.
Вариант 85
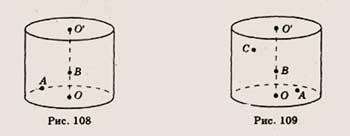
6. Точка А принадлежит основанию цилиндра, изображенного на рисунке 108, а точка
В — оси ОО' этого цилиндра. Скопируйте рисунок и отметьте точку С, в которой
прямая AS пересекает боковую поверхность цилиндра.
7. Полукруг свернут в виде боковой поверхности конуса. Радиус основания конуса
равен 5 см. Найдите объем конуса.
Вариант 86
6. Точка А принадлежит основанию цилиндра, изображенного на рисунке 109, а точка
В — оси ОО' этого цилиндра. Скопируйте рисунок и определите, где, внутри или
снаружи цилиндра, расположена точка С прямой АВ.
7. Диагональ квадрата ABCD равна 10 см. Отрезок AM перпендикулярен плоскости
квадрата, Z ASM = 60°. Найдите расстояние от точки М до прямой BD.
Вариант 87
6. В кубе ABCDA'B'C'D' проведено сечение через середины ребер AS и AD и вершину
С'. Каким многоугольником является это сечение? Сделайте рисунок и отметьте
равные стороны этого многоугольника.
7. Найдите площадь боковой поверхности тела, полученного при вращении прямоугольного
треугольника с катетами 4 см и 7 см, вокруг большего катета.
Вариант 88
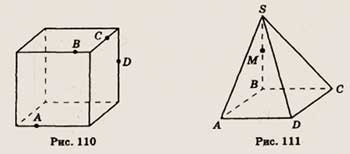
6. Точки А, В, С и D лежат на ребрах изображенного на рисунке 110 куба. Скопируйте
рисунок и определите, пересекаются ли отрезки АС и BD.
7. Ромб со стороной 5 см и углом 60° вращается вокруг своей меньшей диагонали.
Определите объем тела вращения.
Вариант 89
6. В основании пирамиды SABCD, изображенной на рисунке 111, лежит прямоугольник.
Точка М принадлежит ребру SB. Скопируйте рисунок и отметьте на ребре SC точку
N так, чтобы отрезки AN и DM пересекались.
7. Площадь сечения шара плоскостью, проходящей через его центр, равна 4я см
. Найдите объем шара.
Вариант 90
6. Сечение правильной треугольной призмы АВСА'В'С' проходит через ребро АВ и
точку пересечения диагоналей грани АСС'А'. Каким многоугольником является это
сечение? Сделайте рисунок и отметьте равные стороны этого многоугольника.
7. Диагональ осевого сечения цилиндра равна 8 см и наклонена к плоскости основания
цилиндра под углом 30°. Найдите площадь полной поверхности цилиндра.
Вариант 91
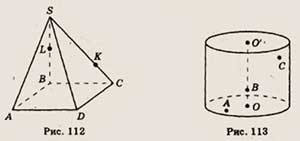
6. В основании пирамиды SABCD, изображенной на рисунке 112, лежит прямоугольник.
Точка L принадлежит ребру SB, а'точка К — ребру SC. Скопируйте рисунок и отметьте
на ребре CD точку М так, чтобы отрезки АК и LM пересекались.
7. Образующая конуса равна 4 см, а угол при вершине осевого сечения равен 90°.
Найдите объем конуса.
Вариант 92
6. Точка А принадлежит основанию цилиндра, изображенного на рисунке 113, а точка
В — оси ОО' этого цилиндра. Скопируйте рисунок и определите, где, внутри или
снаружи цилиндра, расположена точка С прямой AS.
7. Катеты СА и СВ прямоугольного треугольника ABC равны 6 см и 8 см. Через вершину
прямого угла С проходит плоскость, параллельная AS. Меньший катет треугольника
образует с этой плоскостью угол в 45°. Найдите синус угла, который образует
с ней другой его катет.
Вариант 93
6. Точки К, L и М — центры трех видимых граней куба, изображенного на рисунке
114. Скопируйте рисунок и определите, пересекаются ли отрезки DL и КМ.
7. Площадь полной поверхности прямоугольного параллелепипеда, в основании которого
прямоугольник со сторонами 9 см и 6 см, равна 408 см . Найдите диагонали параллелепипеда.
Вариант 94
6. В правильной четырехугольной пирамиде проведено сечение через середины двух
смежных сторон основания и середину высоты пирамиды. Каким многоугольником является
это сечение? Сделайте рисунок и отметьте равные стороны этого многоугольника.
7. Радиус основания цилиндра равен 8 см, площадь боковой поверхности вдвое меньше
площади основания. Найдите площадь полной поверхности цилиндра.
Вариант 95
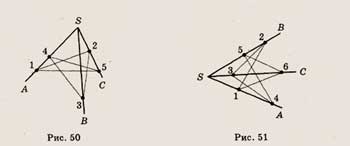
6. Точки А, В и С лежат на видимой части боковой поверхности конуса, изображенного
на рисунке 115. Один из отрезков с концами в этих точках полностью принадлежит
поверхности конуса. Сделайте рисунок и проведите этот отрезок.
7. В правильной четырехугольной пирамиде сторона основания равна 8 см, а боковое
ребро наклонено к плоскости основания под углом 45°. Найдите объем пирамиды.
Вариант 96
6. В правильной треугольной пирамиде SABC проведено сечение через середины ребер
АВ и ВС параллельно ребру SC. Каким многоугольником является это сечение? Сделайте
рисунок и отметьте равные стороны многоугольника.
7. Радиус основания цилиндра равен 4 см, высота в два раза больше длины окружности
основания. Найдите объем цилиндра.